Pseudo-R² (engl.: Pseudo-R² oder Pseudo-R-Square)

Als Pseudo-R² bezeichnet man Maßzahlen – entwickelt für statistische Modelle, die auf Maximum Likelihood-Schätzungen basieren (vor allem für die logistische Regression und verwandte Verfahren) – die sich in Analogie zum R² der linearen Regression als Maß der "Erklärungskraft" des Modell verstehen lassen. Es ist jedoch zu beachten, dass die hier behandelten Maßzahlen häufig kein Maximum von 1 erreichen können; im allgemeinen kann man Pseudo-R²-Werte von 0,2 bis 0,4 bereits als Indikatoren einer sehr guten Erklärungskraft auffassen (das gilt insbesondere für die erste, bekannteste Maßzahl).

Die wohl gebräuchlichsten Maßzahlen sind die folgenden:

Mc-Faddens Pseudo-R² wird berechnet nach der Formel

Dabei ist LL₀ die Log-Likelihood des sog. Nullmodells (eines Modells, welches nur die Regressionskonstante enthält) und LL₁ die Log-Likelihood des zu evaluierenden Modells (also des geschätzten Modells mit meist mehreren Parametern, dessen Güte man beurteilten möchte).

In Analogie zum "korrigierten R²" der linearen Regression, das auch die Zahl der Regressionsparameter und die Fallzahl berücksichtigt, werden entsprechende Versionen für Mc-Faddens Pseudo-R² vorgeschlagen. Soweit ich sehe, ist die Diskussion nicht abgeschlossen und es finden sich sehr viele Vorschläge. Eine der vielen Versionen von Mc-Faddens Pseudo-R² (korrigiert) wird berechnet als

m ist die Zahl der Modellparameter (ohne Konstante). Diese korrigierte Variante soll gewährleisten, dass bei Hinzufügen weiterer Variablen die Pseudo-R²-Größe nur dann zunimmt, wenn LL₁ pro hinzugefügter Variable um mehr als den Betrag von 1 wächst. Sie geht m.W. auf Ben-Akiva und Lerman (1985) zurück.

Das Cox-Snell Pseudo-R² wird berechnet als

Dabei ist L₀ die Likelihood (nicht: Log-Likelihood!) des sog. Nullmodells (eines Modells, welches nur die Regressionskonstante enthält) und L₁ die Likelihood des zu evaluierenden Modells (also des geschätzten Modells mit meist mehreren Parametern, dessen Güte man beurteilten möchte); LR schließlich (in der alternativen Berechnungsvariante) ist das Ergebnis des Likelihood-Verhältnis-Tests für den Vergleich des zu evaluierenden Modells mit dem Nullmodell.

Da das mögliche Maximum des Pseudo-R² nach Cox und Snell meist kleiner 1 ist, wurde noch folgende Größe vorgeschlagen, die das Cox-Snell Pseudo-R² in Beziehung zu seinem jeweiligen theoretischen Maximum setzt; damit kann bei "perfektem" Modell-Fit doch ein Wert von 1 erreicht werden:

Nagelkerkes Pseudo-R², berechnet als

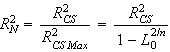
Nagelkerke Pseudo-R-Quadrat

In zwei Papieren von Ernest Shtatland und Koautoren findet sich eine gute Diskussion der hier angesprochenen Maßzahlen. Die Papiere richten sich primär an die Nutzer des Statistikpakets SAS, lassen sich aber völlig unabhängig davon verstehen. (Download als PDF-Datei: Papier 1 [Download von externem Server, Online-Verbindung erforderlich!] und Papier 2.)

Zu beachten ist: Unterschiedliche Modelle können hinsichtlich ihrer Erklärungskraft anhand von Pseudo-R²-Maßen nur dann verglichen werden, wenn es sich um »geschachtelte« Modelle handelt, also solche, von denen eines ein Teilmodell oder Untermodell des jeweils anderen ist. Zum Vergleich nicht-geschachtelter Modelle können z.B. die Größen AIC oder BIC verwendet werden.

Literatur:

Ben-Akiva, M./Lerman, S.: Discrete Choice Analysis: Theory and Application to Travel Demand. Cambridge, MA: MIT-Press, 1985