Varianz (engl.: Variance)

Die Varianz

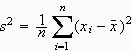
ist die Summe der quadrierten Abweichungen der einzelnen Werte eines Datenbündels vom Mittelwert, dividiert durch n, d.i. durch die Anzahl der Beobachtungen. Die V. ist also ein Maß dafür, wie weit die einzelnen Werte im Durchschnitt von Mittelwert entfernt liegen; es handelt sich mithin um ein Streuungsmaß.

Die oben angegebene Formel charakterisiert ein gegebenes Datenbündel. Handelt es sich bei den Daten um eine Stichprobe und soll ein Schätzwert für die Varianz in der Grundgesamtheit berechnet werden, so wird statt dessen die Größe

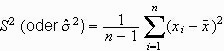
herangezogen.

Wichtiger Hinweis: Hinsichtlich der sprachlichen Bezeichnung der beiden angegebenen Berechnungsmöglichkeiten für die Varianz hat sich leider eine offensichtlich unaufhebbare Konfusion eingebürgert. Wie man durch eine schnelle Internetrecherche ebenso wie durch einen vergleichenden Blick in eine Reihe von Lehrbüchern feststellen kann, werden die Begriffe »empirische Varianz«, »Stichprobenvarianz« und manchmal auch nur »Varianz« alternativ für beide Formeln verwendet. Es kann also vorkommen, dass ein Buch oder eine sonstige Quelle den Begriff »empirische Varianz« für die erste und den Begriff »Stichprobenvarianz« für die zweite Formel verwendet und das nächste Buch genau umgekehrt verfährt! Wieder andere geben nur die eine oder die andere Formel an, ohne auf deren exakte Bedeutung hinzuweisen. Beim Konsultieren statistischer Texte ist also höchte Vorsicht geboten und es ist dringend erforderlich, sich jeweils ein genaues Bild darüber zu verschaffen, was mit »Varianz«, »empirischer Varianz« oder »Stichprobenvarianz« jeweils gemeint ist.

Ein Konfidenzintervall für die Varianz in einer Grundgesamtheit lässt sich mit einer Irrtumswahrscheinlichkeit von α folgendermaßen bestimmen:

Untere Grenze:

Obere Grenze:

Dabei ist das alpha/2-Quantil der Chi-Quadrat-Verteilung mit n-1 Freiheitsgraden (n=Zahl der Untersuchungseinheiten); analoges gilt für den Nenner der ersten Formel.

Die V. kann sinnvollerweise nur bei metrischen Daten (siehe Messniveau) berechnet werden. Jedoch lassen sich Abwandlungen davon als allgemeine Ausdrücke der »Variabilität« von Daten auch auf andere Daten anwenden.

Bitte beachten: Die hier vorgestellten Formeln gelten nur, wenn die Daten eine einfache Zufallsstichprobe darstellen. Bei komplexeren Stichprobendesigns müssen sie entsprechend modifiziert werden; die Details überschreiten den Rahmen dieses Lexikons.

Siehe auch: Standardabweichung