Säulendiagramm (engl.: [Vertical] Bar Chart), Balkendiagramm (engl.: [Horizontal] Bar Chart)
Säulen- oder Balkendiagramme werden zur Darstellung der Verteilung einer diskreten oder gruppierten Variablen (univariates Säulendiagramm) und (seltener) zur Darstellung des Zusammenhanges zwischen zwei diskreten oder gruppierten Variablen eingesetzt. Für jede Ausprägung der Variablen (bei zwei Merkmalen: für jede Ausprägung der Variablenkombination) wird eine Säule bzw. ein Balken abgetragen, dessen Höhe der absoluten oder relativen Häufigkeit der Ausprägung entspricht.
Univariater Fall
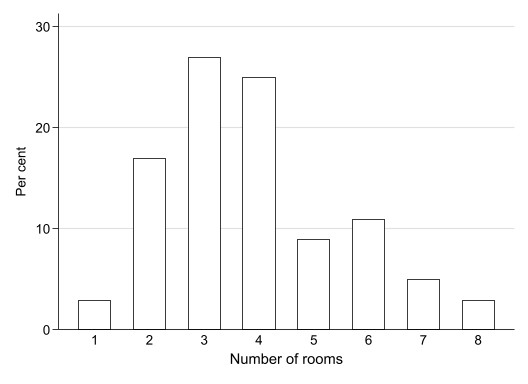
Die beiden folgenden Graphiken zeigen die Verteilung der Antworten aus einer Umfrage auf die Frage nach der Anzahl der Räume der Wohnung der Befragten (100 Datenwerte, simuliert in Anlehnung an einen echten Datensatz).
Zunächst das Säulendiagramm. Man kann ablesen, dass weniger als fünf Prozent der Haushalte nur über einen einzigen Raum verfügen, ca. 17 Prozent über zwei Räume, usw. Wenn die Kenntnis der exakten Datenwerte wichtig ist, können diese zusätzlich oberhalb oder innerhalb der Säulen angezeigt werden; allerdings ist die Aufgabe einer Graphik in der Regel nicht die Darstellung exakter Werte (dafür wäre eine Tabelle mit Zahlen besser), sondern die Vermittlung eines visuellen Eindrucks (etwa, dass 3- und 4-Zimmer-Wohnungen relativ gesehen am häufigsten sind, und zwar viel häufiger als Wohnungen mit einem oder mit 7 oder 8 Zimmern).
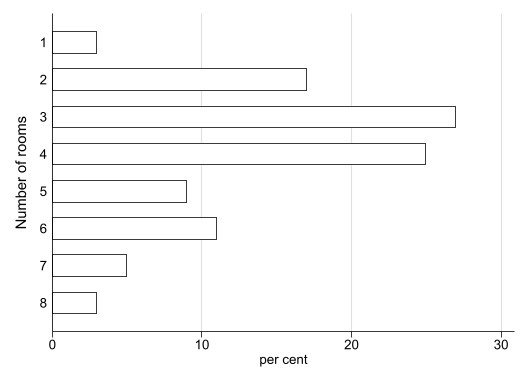
Hier ist das gleiche Diagramm um 90 Grad gedreht. Da die Säulen nicht mehr stehen, werden sie in diesem Fall als Balken bezeichnet.
Bivariater Fall
Im Folgenden werden vier Beispiele gezeigt: Ein (zweidimensionales) gruppiertes Säulendiagramm, ein ebensolches gestapeltes Säulendiagramm, ein (per definitionem fehlerhaftes) Pseudo-3D-Säulendiagramm (ebenfalls gestapelt) und ein dreidimensionales Säulendiagramm zur Darstellung eines zweidimensionalen Zusammenhanges. Die beiden letzteren Diagramme werden hier gezeigt, weil ihre Verwendung durch weit verbreitete schlechte Tabellenkalkulationsprogramme nahegelegt wird. Vom Pseudo-3-D-Diagramm ist jedoch generell abzuraten, und das (echt) dreidimensionale Diagramm sollte nur mit großer Vorsicht und unter den richtigen Bedingungen eingesetzt werden, nämlich dann, wenn es tatsächlich die gemeinsame Verteilung der beiden Merkmale abzulesen erlaubt.
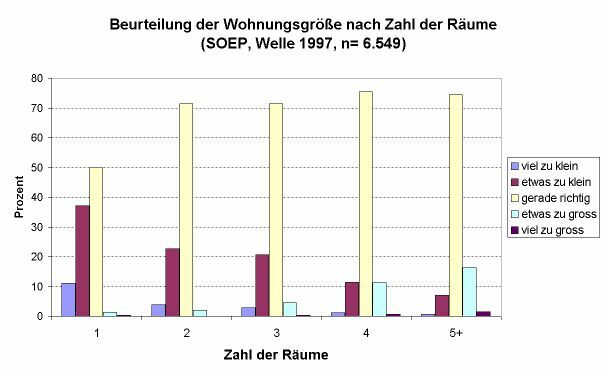
Beispiel für ein gruppiertes zweidimensionales Säulendiagramm
Hier werden für jede Kategorie der ›unabhängigen Variablen‹ (der Wohnungsgröße, hier als Zahl der Zimmer/Räume angegeben) nebeneinander die Anteilswerte der Antworten auf die Frage abgetragen, ob man die Wohnung als zu klein, richtig oder zu groß empfindet. (Es ist zu beachten, dass die Gesamtzahl der in der Wohnung lebenden Personen in dieser Auswertung nicht berücksichtigt ist.) Der Zusammenhang zwischen der Zahl der Räume und Beurteilung der Wohnungsgröße ist zu erkennen, jedoch nicht auf den ersten Blick. Dagegen erschließt sich sehr schnell, dass die Antwort »gerade richtig« bei weitem am häufigsten gegeben wird (und zwar unabhängig von der Wohnungsgröße), während vor allem die Antwort »(viel zu) groß« ziemlich selten ist. Auch die (ungefähre) numerische Ausprägung der verschiedenen Anteilswerte lässt sich recht einfach ablesen.
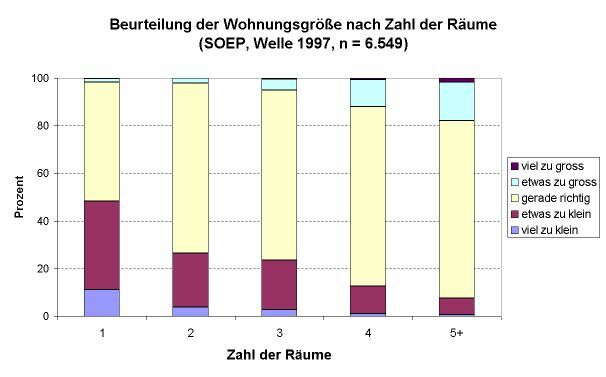
Beispiel für ein gestapeltes zweidimensionales Säulendiagramm
Hier werden für jede Kategorie der ›unabhängigen Variablen‹ übereinander die Anteilswerte der Antworten auf die Frage abgetragen, ob man die Wohnung als zu klein, richtig oder zu groß empfindet. Der Zusammenhang zwischen der Zahl der Räume und Beurteilung der Wohnungsgröße ist hier gut zu erkennen. Dagegen ist es schwerer, die Anteilswerte der einzelnen Antworten abzulesen.
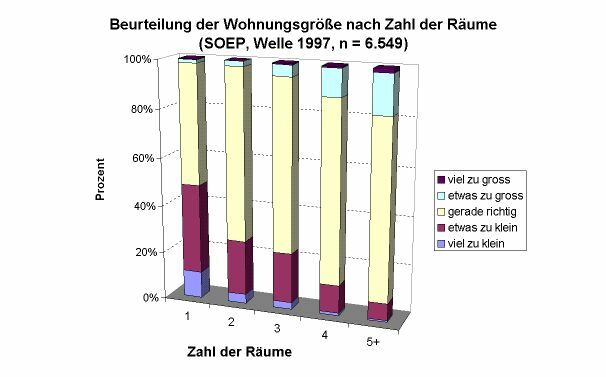
Beispiel für ein gestapeltes pseudo-dreidimensionales Säulendiagramm
Hier werden für jede Kategorie der ›unabhängigen Variablen‹ übereinander die Anteilswerte der Antworten auf die Frage abgetragen, ob man die Wohnung als zu klein, richtig oder zu groß empfindet. Durch die pseudo-dreidimensionale Darstellung wird das Ablesen der Anteilswerte der einzelnen Ausprägungen, bei gestapelten Säulendiagrammen ohnehin nicht leicht, zusätzlich erschwert. Schon aus diesem Grund ist ein solches Diagramm grundsätzlich als fehlerhaft einzustufen. Die dritte Dimension trägt auch keinerlei Information. Die Grafik hat eine ungünstige Data-Ink Ratio.
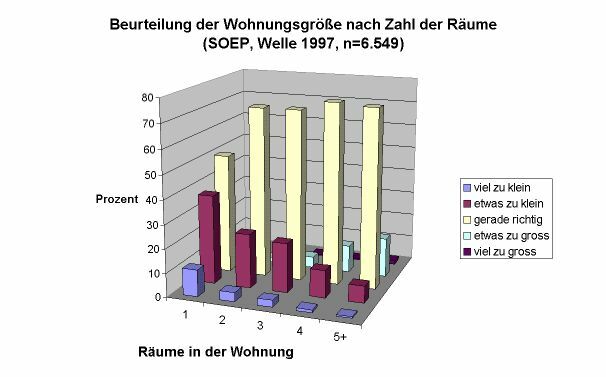
Beispiel für ein dreidimensionales Säulendiagramm zur Darstellung eines zweidimensionalen Zusammenhangs
Hier werden für jede Kategorie der ›unabhängigen Variablen‹ hintereinander die Anteilswerte der Antworten auf die Frage abgetragen, ob man die Wohnung als zu klein, richtig oder zu groß empfindet. Durch die dreidimensionale Darstellung wird das Ablesen der Anteilswerte der einzelnen Ausprägungen verhindert, und zwar nicht nur bei jenen Säulen, die durch höhere Säulen im Vordergrund verdeckt werden, sondern auch für die sichtbaren Säulen (die vier rechten gelben Säulen haben alle Werte von über 70 Prozent!).
Man kann ein solches Diagramm auch anders interpretieren: als Darstellung der gemeinsamen Wahrscheinlichkeitsfunktion der beiden Variablen (in diesem Fall müssten sich allerdings die Prozentwerte über alle Säulen zu 100 addieren und nicht die pro Ausprägung der unabhängigen Variablen). Auch wenn eine solche Verwendung des Diagramms im Grundsatz richtig ist, bleibt das Problem der möglicherweise fehlenden oder zumindest schlechten Ablesbarkeit der Datenwerte bestehen.
© W. Ludwig-Mayerhofer, ILMES | Last update: 23 Jan 2025