Levene-Test (auch: Levenes Test, engl.: Levene's test) auf Varianzgleichheit

Mit dem L. kann geprüft werden, ob die Varianzen zweier oder mehrerer Gruppen gleich sind. Es wird also die Nullhypothese, dass alle Varianzen gleich sind, gegen die Alternativhypothese geprüft, dass mindestens eine der geprüften Varianzen sich von der oder den anderen unterscheidet.

In einer Stichprobe des Umfangs n und mit den Umfängen der k Unterstichproben (der einzelnen Gruppen) n_i ist die Statistik

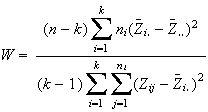
F-verteilt mit k-1 und n-k Freiheitsgraden. Dabei kann Z_ij für eine der drei folgenden Größen stehen:

mit als dem arithmetischen Mittel der i-ten Gruppe.

mit als dem Median der i-ten Gruppe.

mit als dem (meist: 10 %) getrimmten arithmetischen Mittel der i-ten Gruppe.

Schließlich sind die die Gruppenmittelwerte von Z_ij und der Mittelwert von Z_ij über alle Gruppen.

Levene hat nur die erste der drei Definitionen von Z_ij vorgeschlagen. Wenn die Daten sehr schief verteilt sind, haben die beiden anderen Varianten bessere Testeigenschaften.

Hinweis: SPSS wendet in der Prozedur "t-test" nur die erste Definition von Z_ij an. Im Kontext der explorativen Datenanalyse (Prozedur EXAMINE) sind auch die anderen Varianten verfügbar.

Eine Alternative zum Levene-Test ist beispielsweise der Bartlett-Test. Dieser kann vor allem dann zur Anwendung kommen, wenn die Daten einigermaßen normalverteilt sind.