Schiefe (engl.: Skewness)

Die S. einer Verteilung gibt an, wie stark die Verteilung der Datenwerte von einer symmetrischen Verteilung abweicht. Man spricht von einer rechtsschiefen (oder linkssteilen) Verteilung, wenn der Schwerpunkt der Verteilung sozusagen "nach links verschoben" ist. (In diesem Fall ist der Mittelwert der Verteilung auch größer als der Median, zumindest wenn es sich um eine eingipflige Verteilung handelt.) Im umgekehrten Fall spricht man von einer linksschiefen bzw. rechtssteilen Verteilung. Angaben zur Schiefe einer Verteilung sind nur bei eingipfliger Häufigkeitsverteilung sinnvoll.

Zur Messung der S. gibt es verschiedene Maßzahlen; die meisten davon beziehen sich auf das "dritte Moment" der Verteilung, d.h. auf die in die 3. Potenz erhobenen Abweichungen der einzelnen Datenwerte vom Mittelwert. Für diese Maßzahlen gilt im Regelfall: Ist der Wert gleich Null, ist die Verteilung symmetrisch, bei einer linkssteilen Verteilung ist der Wert größer als Null, bei einer rechtssteilen Verteilung ist er kleiner als Null. Ersichtlich ist eine Berechnung dieser Maßzahlen nur bei metrischen Variablen (siehe Messniveau) legitim. Eine Maßzahl zur Beurteilung der Schiefe einer Verteilung ist der Momentenkoeffizient der Schiefe:

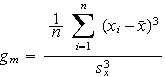
Formel Momentenkoeffizient

Genaueren Aufschluss über die Schiefe einer Verteilung erhält man durch graphische Darstellungen. So vermitteln z.B. Quantil-Plots einen guten visuellen Eindruck der Verteilung.
Ein typisches Beispiel für eine rechtsschiefe bzw. linkssteile Verteilung sind Einkommensverteilungen: der größte Teil der Einkommen liegt im unteren und mittleren Bereich, nur relativ wenige liegen im oberen Bereich.

Einen ersten Eindruck kann ein Histogramm geben (verwendet wurden Daten des SOEP 2002):

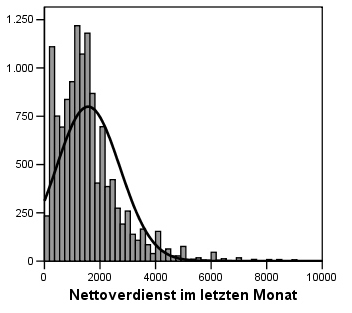
Histogramm Einkommen

Im entsprechenden Quantil-Plot ist gut zu erkennen, dass sich der größte Teil der Verteilung im unteren Einkommensbereich konzentriert:

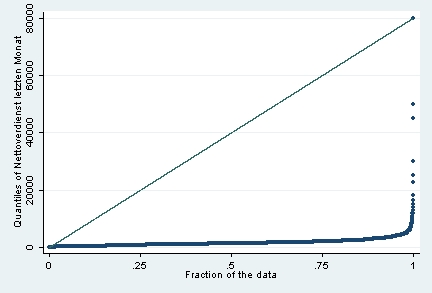
Quantil-Plot Einkommen

Statt die Häufigkeitsverteilung der Beobachtungen einer Variable direkt mit einer Normalverteilung zu vergleichen, werden in einem so genannten Normal-Quantil-Plot die Quantile der Häufigkeitsverteilung mit den entsprechenden Quantilen der Standardnormalverteilung verglichen. Wenn die Verteilung linkssteil ist, wie in unserem Beispiel, ist der NQ-Plot in der Tendenz konvex und die Punkte liegen über der Geraden:

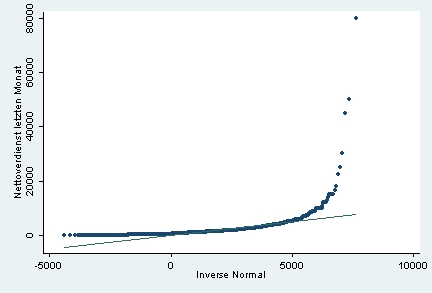
Normal-Quantil-Plot Einkommen

Bei einer rechtssteilen Verteilung ist der NQ-Plot entsprechend konkav, bei einer annähernd standard-normalverteilten Verteilung liegen die Punkte des NQ-Plots nahe an oder auf der Geraden.

Der Schiefe-Koeffizient beträgt entsprechend 15,44.