Arithmetisches Mittel (engl.: Arithmetic Mean)

Lagemaß zur Kennzeichnung von metrischen (also mindestens intervallskalierten) Daten. Oft auch einfach als "Mittelwert" bezeichnet, was streng genommen wegen der Existenz anderer Mittelwerte (etwa geometrisches oder harmonisches Mittel) nicht korrekt ist, aber sicher dann zulässig, wenn aus dem Kontext eindeutig hervorgeht, was gemeint ist. Es wird berechnet als:

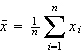
Formel aritmethisches Mittel

Das bedeutet, dass die Summe der Einzelwerte des Datenbündels durch die Zahl der Elemente dividiert wird.

Werden die kleinsten und größten Werte des Datenbündels von der Berechnung ausgeschlossen, so spricht man vom getrimmten a. M. (z.B. 5-%-getrimmtes Mittel, wenn die 5 % kleinsten und 5 % größten Werte weggelassen werden). Dies kann als sinnvoll erachtet werden, um den Einfluss extremer Werte auf das a. M. zu reduzieren.

Schätzung:

Liegen Stichprobendaten vor, so gilt der nach der obigen Formel berechnete Stichprobenmittelwert auch als beste Schätzung für den Mittelwert in der Grundgesamtheit. Konfidenzintervalle mit der Irrtumswahrscheinlichkeit α können nach folgenden Formeln berechnet werden:

1. Wenn die Varianz der Grundgesamtheit bekannt ist und das Merkmal X entweder normalverteilt ist oder wenn bei beliebiger Verteilung von X eine Stichprobengröße von mindestens n=30 vorliegt, so hat das Konfidenzintervall die Unter- und Obergrenze

mit als dem Wert des (1-α/2)-Quantils der Standardnormalverteilung.

2. Ist die Varianz von X in der Grundgesamtheit unbekannt und der Stichprobenumfang n ausreichend groß (n>30), so werden die Unter- und Obergrenze des Konfidenzintervalls als

berechnet. Dabei ist der Schätzer für die Varianz in der Grundgesamtheit.

3. Ist die Varianz von X in der Grundgesamtheit unbekannt und der Stichprobenumfang n klein, so können bei normalverteiltem Merkmal X die Unter- und Obergrenze des Konfidenzintervalls als

berechnet werden. Dabei ist der Schätzer für die Varianz in der Grundgesamtheit und der Wert des (1-α/2)-Quantils der t-Verteilung mit n-1 Freiheitsgraden.