Exzess (engl.: Kurtosis)

Sorry, nichts Aufregendes oder gar Unanständiges: Der E., auch Wölbung genannt, beschreibt, wie »flach« oder »steil« eine Verteilung im Vergleich zu einer Normalverteilung ist. Angaben zur Wölbung einer Verteilung sind nur bei eingipfliger Häufigkeitsverteilung sinnvoll.

Zur Messung des E. gibt es verschiedene Maßzahlen; die meisten davon beziehen sich auf das »vierte Moment« der Verteilung, d.h. auf die in die 4. Potenz erhobenen Abweichungen der einzelnen Datenwerte vom Mittelwert. Für diese Maßzahlen gilt im Regelfall: Liegt der Wert um Null, ist das Datenbündel in etwa normalverteilt, ist der Wert größer als Null, ist die Verteilung spitzer, ist er kleiner als Null, ist sie flacher als eine Normalverteilung. Ersichtlich ist eine Berechnung dieser Maßzahlen nur bei metrischen Variablen (siehe Messniveau) legitim.
Die Maßzahlen sollen charakterisieren, wie stark oder schwach der zentrale Bereich oder die Randbereiche der Daten besetzt sind.

Eine gebräuchliche Maßzahl ist das Wölbungsmaß von Fisher, das so definiert ist, dass es bei einer Normalverteilung gerade den Wert Null annimmt:
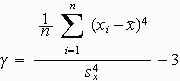
Formel Fisher-Wölbungsmaß

Genaueren Aufschluss über die Wölbung einer Verteilung erhält man anhand graphischer Darstellungen. So vermitteln z.B. Quantil-Plots einen guten visuellen Eindruck der Verteilung.
Als Beispiel für eine flache Verteilung wird hier ein fiktiver Datensatz verwendet, der Angaben zur Körpergröße enthält.

Einen ersten Eindruck kann ein Histogramm geben:

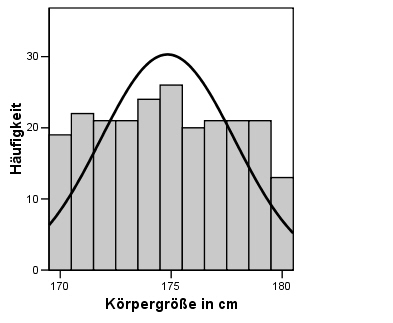
Wölbung Histogramm

Statt die Häufigkeitsverteilung der Beobachtungen einer Variable direkt mit einer Normalverteilung zu vergleichen, werden in einem so genannten Normal-Quantil-Plot die Quantile der Häufigkeitsverteilung mit den entsprechenden Quantilen der Standardnormalverteilung verglichen.
Wenn die Verteilung wie in unserem Beispiel nun eine geringere Wölbung hat, erhält man folgenden NQ-Plot:

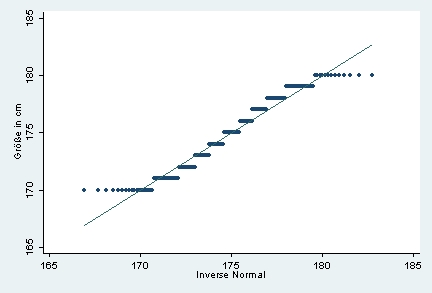
Wölbung NQ-Plot

Die Berechnung des Wölbungsmaßes ergibt entsprechend -1.135.