(Wilcoxons) Rangsummentest (engl: [Wilcoxon's] Rank-Sum Test)
Der Rangsummentest nach Wilcoxon ist ein nichtparametrisches Verfahren zum Vergleich zweier Stichproben; er testet, ob die Werte einer der beiden Gruppen tendenziell größer (oder kleiner) als die der anderen Gruppe sind (wobei sich »Gruppe« hier auf die Grundgesamtheiten bezieht, aus der die Stichproben stammen). Es handelt sich somit um eine Alternative zum t-Test, die vor allem dann angewendet werden sollte, wenn dessen Anwendungsvoraussetzungen stark verletzt sind, d.h. wenn die Messwerte nicht normalverteilt oder die Varianzen der beiden Gruppen stark unterschiedlich sind oder sogar beides gegeben ist; unterschiedliche Gruppengrößen können ein zusätzliches Problem sein.
Der Rangsummentest vergleicht statt der Original-Messwerte die Rangwerte der Daten. Er prüft letztlich, ob die Zahl der Beobachtungen, die kleiner (oder größer) als der gemeinsame Median beider Gruppen sind, in den beiden Gruppen verschieden ist.
Zur Berechnung des Wilcoxon-Tests werden die Originaldaten durch die entsprechenden Rangplätze ersetzt, die sich bei Ordnung der Datenwerte der Größe nach ergeben. Im Beispiel (fingierte Einkommensdaten) sieht das etwa so aus:
| Gruppe 1 | Gruppe 2 | ||
|---|---|---|---|
| Originalwert | Rangplatz | Originalwert | Rangplatz |
| 1700 | 1 | 2100 | 3 |
| 2000 | 2 | 2400 | 4 |
| 2700 | 5 | 2800 | 6 |
| 3500 | 7 | 4400 | 8 |
(Ob der Rangplatz 1 den kleinsten oder den größten Wert kennzeichnet ist gleichgültig, solange man weiß was man tut; SPSS verfährt z.B. so wie ich im obigen Beispiel.)
Anschließend wird für eine der beiden Gruppen – im folgenden als Gruppe 1 bezeichnet – die Summe der Rangplätze in dieser Gruppe ermittelt. (Oft wird in der Literatur als »Gruppe 1« die Gruppe mit der kleineren Rangsumme bezeichnet, und auch das Statistik-Software-Paket SPSS verfährt so. M.E. führt das eher zur Verwirrung, weil im Falle des unten aufgeführten Tests nach der Normalverteilung stets eine negative Teststatistik resultiert; aber im Grunde ist es kein echtes Problem. Die Empfehlung stammt aus der Zeit, als man noch per Hand rechnete.)
Das weitere Verfahren hängt nun von bestimmten Voraussetzungen ab:
1. Sind die untersuchten Stichproben klein, so muss die ermittelte Summe der Rangplätze – oft als W bezeichnet – mit entsprechenden kritischen Werten verglichen werden, die in manchen Statistik-Lehrbüchern tabelliert sind. Was »klein« heißt, wird in der Literatur unterschiedlich definiert: Manche sprechen davon, dass der Umfang jeder Gruppe mindestens acht Fälle betragen muss, andere von mindestens 20 Fällen pro Gruppe, wieder andere von mindestens 25 Fällen in einer der beiden Gruppen.
2. Sind die untersuchten Stichproben groß genug, d.h. überschreiten sie die unter 1. genannten Grenzen, so folgt die Statistik
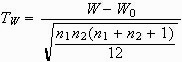
einer Standardnormalverteilung. Dabei ist
W die Summe der Rangplätze in Gruppe 1,
W0 die unter der Nullhypothese, dass keine Mittelwertunterschiede bestehen, zu erwartende Rangsumme, zu berechnen nach der Formel
![]() , und
, und
n1 bzw. n2 ist der Umfang von Gruppe 1 bzw. Gruppe 2.
Treten »Bindungen« (engl: »Ties«), d.h. gleiche Werte (und damit gleiche Ränge) über die beiden Gruppen hinweg auf, so wird allen betreffenden Fällen das arithmetische Mittel der betreffenden Rangplätze zugewiesen. Gibt es viele Bindungen, so wird die Gültigkeit der oben genannten Formel eingeschränkt; über alternative Formeln informieren manche Lehrbücher.
Liegen mehr als zwei Gruppen vor, kann der Kruskal-Wallis H-Test verwendet werden.
© W. Ludwig-Mayerhofer | Last update: 11 Apr 2025