(Binäre) Logistische Regression (engl.: [Binary ]Logistic Regression)

Logistischer Regression ist ein Verfahren zur multivariaten Analyse nicht-metrischer abhängiger Variablen. Dieser Artikel behandelt die binäre Regression, d.h. den Fall einer abhängigen Variablen mit zwei Ausprägungen. Die Einflüsse auf solche Variablen können nicht mit dem Verfahren der linearen Regressionsanalyse untersucht werden, da wesentliche Anwendungsvoraussetzungen insbesondere in inferenzstatistischer Hinsicht (Normalverteilung der Residuen, Varianzhomogenität) nicht gegeben sind. Ferner kann ein lineares Regressionsmodell bei solchen Variablen zu unzulässigen Vorhersagen führen: Wenn man die beiden Ausprägungen der abhängigen Variablen mit 0 und 1 kodiert, so kann man zwar die Vorhersage eines linearen linearen Regressionsmodells als Vorhersage der Wahrscheinlichkeit auffassen, dass die abhängige Variable den Wert 1 annimmt – formal: P(Y=1) –, doch kann es dazu kommen, dass Werte außerhalb dieses Bereichs vorhergesagt werden.

Die logistische Regression löst dieses Problem durch eine geeignete Transformation der abhängigen Variablen P(Y=1). Sie geht aus von der Idee der Odds, d.h. dem Verhältnis von P(Y=1) zur Gegenwahrscheinlichkeit 1-P(Y=1) bzw. P(Y=0) (bei Kodierung der Alternativkategorie mit 0)

Die Odds können zwar Werte >1 annehmen, doch ist ihr Wertebereich nach unten beschränkt (er nähert sich asymptotisch 0 an). Eine unbeschränkter Wertebereich wird durch die Transformation der Odds in die sog. Logits

erzielt; diese können Werte zwischen minus und plus unendlich annehmen.

In der logistischen Regression wird dann die Regressionsgleichung

geschätzt; es werden also Regressionsgewichte bestimmt, nach denen die geschätzten Logits für eine gegebene Matrix von unabhängigen Variablen X berechnet werden können. Die folgende Graphik zeigt, wie Logits (X-Achse) mit den Ausgangswahrscheinlichkeiten P(Y=1) (Y-Achse) zusammenhängen:

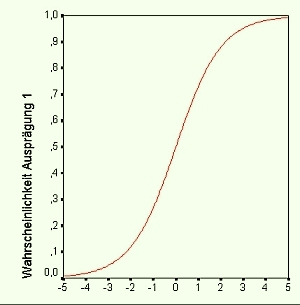
Die Regressionkoeffizienten der logistischen Regression sind nicht sehr anschaulich, da sie die Effekte der Änderung einer unabhängigen Variable um den Betrag 1 auf die Logits angeben. Aus diesem Grund berichtet man häufig die sog. Effektkoeffizienten, die durch Bildung des Antilogarithmus der Logit-Koeffizienten gewonnen werden; die Regressionsgleichung bezieht sich dadurch auf die Odds:

Bei den Effektkoeffizienten exp(b_n) bezeichnen Werte <1 einen negativen Einfluss auf die Odds, ein positiver Einfluss ist gegeben, wenn exp(b_n) >1. Zu beachten ist, dass die Effektkoeffizienten multiplikativ wirken: Ein Koeffizient von bspw. 1,4 besagt, dass die Odds jeweils auf das 1,4-fache oder um 40 Prozent zunehmen, ein Koeffizient von 0,6, dass sie auf das 0,6-fache, also um 40 Prozent abnehmen, wenn die unabhängige Variable um eine Einheit zunimmt.

Durch eine weitere Transformation lassen sich die Einflüsse der logistischen Regression auch als Einflüsse auf die Wahrscheinlichkeiten P(Y=1) ausdrücken:

Die Regressionsparameter werden auf der Grundlage des Maximum Likelihood-Verfahrens geschätzt. Inferenzstatistische Verfahren stehen sowohl für die einzelnen Regressionskoeffizienten als auch für das Gesamtmodell zur Verfügung (siehe Wald-Statistik und Likelihood-Verhältnis-Test); in Analogie zum linearen Regressionsmodell wurden auch Verfahren der Regressionsdiagnostik entwickelt, anhand derer einzelne Fälle mit übergroßem Einfluss auf das Ergebnis der Modellschätzung identifiziert werden können. Schließlich gibt es auch einige Vorschläge zur Berechnung einer Größe, die in Analogie zum R² der linearen Regression eine Abschätzung der Erklärungskraft des Modells erlaubt; man spricht hier von sog. Pseudo-R². Auch das AIC und das BIC werden in diesem Kontext gelegentlich herangezogen.

Als (im wesentlichen gleichwertige) Alternative kann das Probit-Modell (in ILMES noch nicht enthalten) herangezogen werden.

Eine Übertragung der logistischen Regression (und des Probit-Modells) auf abhängige Variable mit mehr als zwei (nominal- oder ordinalskalierten) Merkmalen ist möglich (siehe Multinomiales Logit und Ordinales Logit).

Literatur:

Agresti, Alan: Categorical Data Analysis. New York: Wiley, 1990, 2. Auflage 2002, 3. Auflage 2015
Andreß, Hans-Jürgen/Hagenaars, J.-A./Kühnel, Steffen: Analyse von Tabellen und kategorialen Daten. Berlin u.a.: Springer, 1997