Varianzanalyse (engl.: Analysis of Variance)
Eine Klasse von statistischen Analyseverfahren zur Durchführung von Mittelwertvergleichen zwischen mehreren Gruppen (bei zwei Gruppen siehe auch t-Test).
Werden Mittelwertunterschiede einer (abhängigen) Variablen geprüft, so spricht man von univariater V. (ANOVA), bei simultanen Tests mehrerer abhängiger Variablen von multivariater V. (MANOVA). Werden die Untersuchungspersonen (oder allgemeiner: Untersuchungsobjekte) hinsichtlich eines Merkmals in Gruppen eingeteilt, spricht man von einfaktorieller V. (die Gruppenzugehörigkeit wird auch als Faktor bezeichnet), bei mehreren Gruppierungsmerkmalen von mehrfaktorieller (bzw. konkret zwei-, drei- usw. -faktorieller) V. Bei der mehrfaktoriellen V. können auch Interaktionseffekte geprüft werden, d. h. unterschiedliche Wirkungen eines Faktors in Abhängigkeit von den Ausprägungen eines oder mehrerer anderen Faktors/Faktoren.
Wichtige Spezialfälle sind die V. bei Messwiederholungen sowie die Kovarianzanalyse (ANCOVA) (die Durchführung von Gruppenvergleichen bei simultaner Berücksichtigung des potenziellen Einflusses weiterer, i. a. metrischer Variablen).
Die V. ist wohl das wichtigste statistische Auswertungsverfahren in der Psychologie, da sie sich nicht zuletzt besonders gut für die Auswertung experimenteller Daten eignet. Dieser kurze Einführungsartikel kann der Komplexität der verschiedenen Varianten der V. keinesfalls gerecht werden, hierzu muss auf die ein- und weiterführende Literatur verwiesen werden.
Grundlagen
Die Grundidee der V. besteht darin, die gesamte Varianz des zu erklärenden Merkmals, der abhängigen Variablen (oder mehrerer solcher Variablen) aufzuteilen (zu »zerlegen«) in die Varianz zwischen den Gruppen – die Abweichung der Gruppenmittelwerte vom Gesamtmittelwert über alle Gruppen bzw. Untersuchungseinheiten – und die Varianz innerhalb der Gruppen (die Abweichung der einzelnen Messwerte innerhalb der Gruppen vom Gruppenmittelwert, auch Residualvarianz oder Fehlervarianz genannt). Sind die Unterschiede zwischen den Gruppen relativ groß bei gleichzeitig nicht allzu großer Varianz innerhalb der Gruppen, so kann man davon ausgehen, dass die Gruppenzugehörigkeit einen Einfluss auf die abhängige Variable hat. Einzelheiten dazu im Folgenden bei der Darstellung der wichtigsten Verfahren.
Als Maß für die Erklärungskraft der untersuchten Faktoren (der Determination des abhängigen Merkmals durch die Gruppenzugehörigkeit) steht das PRE-Maß Eta² zur Verfügung.
Voraussetzung für die Gültigkeit der inferenzstatistischen Absicherung der Mittelwertunterschiede ist die Normalverteilung der abhängigen Variablen in der Grundgesamtheit sowie die Gleichheit der Varianzen in den einzelnen Gruppen (Varianzhomogenität). Die Varianzanalyse ist aber einigermaßen robust gegen moderate Verletzungen dieser Annahmen, vor allem wenn die Gruppen nicht zu klein und (in etwa) gleich groß sind (vgl. dazu die einschlägigen Angaben bei Bortz).
Die wichtigsten (einfacheren) Verfahren
Einfaktorielle univariate Varianzanalyse
Hier wird davon ausgegangen, dass die gesamte Variabilität in den Daten sich zerlegen lässt in einen Teil, der auf die Gruppenzugehörigkeit zurückgeht, und eine »Restvariabilität«, die nicht durch die Gruppenzugehörigkeit bestimmt wird. Die auf die Gruppenzugehörigkeit zurückgehende Unterschiedlichkeit der Daten drückt sich aus in der Abweichung der Gruppenmittelwerte vom Gesamtmittelwert, die »Restvariabilität« oder Unterschiedlichkeit innerhalb der Gruppen in der Abweichung der einzelnen Datenwerte vom Gruppenmittelwert. Wenn wir die Gesamtvariabilität als QStotal, die Unterschiedlichkeit zwischen den Gruppen als QSzwischen und die Unterschiedlichkeit innerhalb der Gruppen als QSinnerhalb bezeichnen, so gilt:
![]()
Mathematisch exakt schreiben wir:
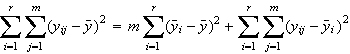
Dabei ist r die Zahl der Gruppen, m die Zahl der Fälle pro Gruppe (wir gehen hier davon aus, dass diese Zahl in allen Gruppen identisch ist), die yij sind die Messwerte der j = 1...m Personen in den i = 1...r Gruppen, und y-quer bzw. yi-quer sind der Gesamtmittelwert bzw. die i Gruppenmittelwerte.
Die »Varianzen« innerhalb der bzw. zwischen den Gruppen werden im Kontext der Varianzanalyse als mittlere Quadratsumme (hier: MQS) bezeichnet. Für die mittlere Quadratsumme zwischen den Gruppen gilt:
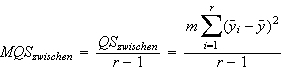
und für die mittlere Quadratsumme innerhalb der Gruppen:
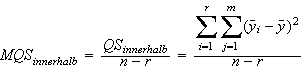
mit n (wie üblich) als der Gesamtzahl aller Untersuchungseinheiten in der Stichprobe.
Die Prüfgröße
![]()
ist dementsprechend F−verteilt mit r-1 und n−r Freiheitsgraden. Sie gibt Auskunft darüber, ob irgendwelche Unterschiede zwischen den Gruppen bestehen (anders formuliert: ob die Gruppen aus der gleichen Grundgesamtheit stammen oder nicht), es handelt sich also um eine globale Teststatistik. Um zu prüfen, ob spezifische Gruppenmittelwerte höher oder niedriger (als der Gesamtmittelwert oder als andere Gruppenmittelwerte) sind, sollte man A-priori-Hypothesen durch Angaben von Kontrasten testen. Es stehen aber auch A-posteriori-Tests zur Verfügung, von denen z. B. der Scheffé-Test empfehlenswert (weil eher konservativ) ist. Die Annahme der Varianzhomogenität wird beispielsweise durch den Bartlett-Test geprüft. (Das Ergebnis dieses Tests sollte nicht signifikant sein , d. h., die Varianzen sollten sich gerade nicht signifikant voneinander unterscheiden).
Mehrfaktorielle univariate Varianzanalyse
Hier können nicht nur die Effekte der einzelnen Faktoren (Haupteffekte), sondern auch gemeinsame Effekte (Interaktionseffekte) geprüft werden. Neben dem globalen F-Test wird für jeden dieser Effekte ein separater F-Test durchgeführt. Dabei ist (am Beispiel der zweifaktoriellen V. erläutert) die Zahl der Freiheitsgrade des Haupteffekts für Faktor A = p−1 (p = Zahl der Gruppen in Faktor A), für Faktor B = q−1 (q = Zahl der Gruppen in Faktor B), für den Interaktionseffekt AxB = (p−1)(q−1) und für die Fehlervarianz n − (p*q).
Prüfungen von Hypothesen über spezifische Effekte einzelner Faktoren sind hier nicht immer ohne weiteres möglich. Sind signifikante Interaktionseffekte vorhanden, ist die Interpretation der Haupteffekte problematisch. Genauer gesagt können wir hier zwischen folgenden Fällen unterscheiden:
Im einfachsten Fall sind nur Haupteffekte vorhanden (natürlich ist auch denkbar dass nur ein einziger Haupteffekt vorhanden ist, dann ergibt sich aber der Fall der einfachen Varianzanalyse). Die folgende Graphik zeigt ein entsprechendes Beispiel: Der Wert von Gruppe 1 liegt konsistent unter dem von Gruppe 2; unter Bedingung 1 zeigen beide Gruppen einen niedrigeren Wert als unter Bedingung 2. Sowohl die Variable »Gruppe« als auch die Variable »Bedingung« haben einen Haupteffekt:
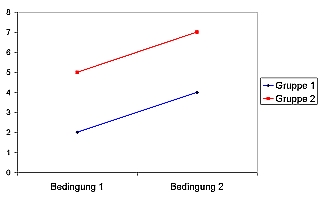
Im nächsten Fall unterscheiden sich die beiden Gruppen 1 und 2 ebenfalls konsistent untereinander; Gruppe 1 hat stets niedrigere Werte als Gruppe 2. Auch führt Bedingung 2 in beiden Gruppen zu höheren Werten der abhängigen Variablen, so dass auch von einem Haupteffekt von »Bedingung« auszugehen ist. Der Unterschied zwischen beiden Gruppen ist jedoch unter Bedingung 2 größer. Man spricht hier von einer ordinalen Interaktion:
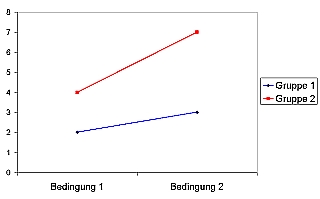
Ein weiterer denkbarer Fall ist der der hybriden Interaktion (siehe folgende Graphik): Gruppe 1 hat stets höhere Werte als Gruppe 2; es ist also ein Haupteffekt von »Gruppe« vorhanden. Doch ist kein klarer Mittelwert-Unterschied zwischen Bedingung 1 und Bedingung 2 zu erkennen; Bedingung 2 wirkt auf die beiden Gruppen in entgegengesetzter Richtung. Der Haupteffekt von »Bedingung« sollte hier nicht interpretiert werden.
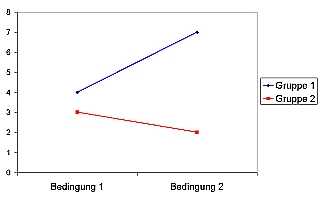
Im Fall einer disordinalen Interaktion (siehe folgende Graphik) sind keinerlei Haupteffekte vorhanden, sondern nur ein Interaktionseffekt: Weder unterscheiden sich die Mittelwerte von Gruppe 1 und Gruppe 2 noch die von Bedingung 1 und Bedingung 2; die Wirkungen der »Gruppenzugehörigkeit« hängen davon ab, welcher Bedingung die Gruppen ausgesetzt sind bzw. umgekehrt.
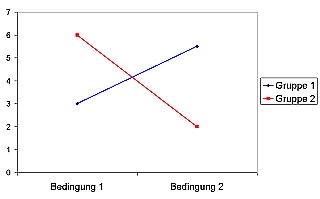
Ferner können Probleme entstehen, wenn (wie es bei nicht-experimentellen Designs häufig der Fall ist) die einzelnen Faktoren nicht voneinander unabhängig sind. In diesem Fall kann die Varianz nicht mehr eindeutig in ihre verschiedenen Anteile zerlegt werden; die Gruppen weisen gemeinsame Varianzanteile auf. Zur Lösung dieses Problems werden verschiedene Strategien angeboten: Bei hierarchischem Faktoreneinschluss wird zunächst der Beitrag des ersten Faktors zur Varianzerklärung geprüft und anschließend derjenige Beitrag des zweiten (und gegebenenfalls weiterer) Faktors/Faktoren, der durch den ersten Faktor noch nicht erfasst wurde. Die gemeinsame Varianzerklärung beider Faktoren wird damit dem ersten Faktor zugeschlagen, und die Ergebnisse können sehr stark von der Reihenfolge des Einschlusses der verschiedenen Faktoren abhängen. Bei simultanem Einschluss der Faktoren wird ähnlich wie beim linearen Regressionsmodell versucht, für jeden Faktor den nur durch diesen Faktor erklärten Varianzanteil zu bestimmen.
Auch Tests spezifischer Kontraste sind hier nicht ohne weiteres durchzuführen, die verfügbaren Statistik-Programme erlauben aber im allgemeinen Tests der Abweichung einzelner Gruppen vom Gesamtmittelwert oder von einer Referenzgruppe und häufig weitere Tests.
Auch bei der mehrfaktoriellen V. ist die Gültigkeit der Annahme der Varianzhomogenität durch eine geeignete Statistik zu testen.
Multivariate Varianzanalyse
Hier verkomplizieren sich die bislang angestellten Überlegungen noch beträchtlich; da es mehrere abhängige Variablen gibt, kann nicht eine Quadratsumme berechnet und für Tests herangezogen werden. Mehrere alternative globale Teststatistiken stehen zur Verfügung, etwa Wilk's Lambda, Hotelling's Spur-Kriterium, Roy's größter Eigenwert oder Pillai's Spur-Kriterium. Auch die Anwendungsvoraussetzungen der Signifikanztests sind komplexer. Es sollte zunächt geprüft werden (mit Bartletts Sphärizitätstest), ob die abhängigen Variablen untereinander zusammenhängen; ist dies nicht der Fall, können statt der multivariaten V. mehrere univariate V.n durchgeführt werden, die leichter zu berechnen und zu interpretieren sind. Ferner ist nicht nur die Homogenität der Varianzen in den einzelnen Gruppen zu prüfen; auch die Kovarianzen zwischen den abhängigen Variablen innerhalb der Gruppen sollen sich (vor allem bei kleineren Stichproben) nicht erheblich voneinander unterscheiden (Prüfung durch Box' M).
Literatur:
- Bortz, Jürgen/Schuster, Christof: Statistik für Human- und Sozialwissenschaftler, 7., vollständig überarbeitete und aktualisierte Auflage. Berlin, Heidelberg, New York: Springer, 2010.
Frühere Auflagen in Alleinautorenschaft von Jürgen Bortz, teilweise unter dem Titel »Statistik für Sozialwissenschaftler« bzw. »Lehrbuch der Statistik für Sozialwissenschaftler«
© W. Ludwig-Mayerhofer, ILMES | Last update: 02 Nov 2010 |