Chi²-Verteilung, Chi²-Test (engl.: Chi-Square Distribution, Test)

Verteilung einer Zufallsvariablen, die für Signifikanztests und zur Berechnung von Konfidenzintervallen eingesetzt werden kann. Sie entsteht durch die Summierung von n quadrierten standardnormalverteilten Zufallsvariablen (sog. z-Variablen). Es gibt also viele verschiedene Chi-Quadratverteilungen, die sich durch die Zahl der aufsummierten z-Variablen unterscheiden. Man spricht in diesem Zusammenhang von den Freiheitsgraden der Chi²-Verteilung; durch Summierung von drei z-Variablen entsteht beispielsweise eine Chi²-Verteilung mit drei Freiheitsgraden. Die Werte von Chi²-Verteilungen mit unterschiedlichen Freiheitsgraden sind in allen Statistiklehrbüchern tabelliert.

Die wichtigsten Anwendungen sind:

1. Anpassungstest für eine kategoriale Variable

Gegeben sei eine empirische Verteilung einer kategorialen (nominalskalierten) Variablen mit I Kategorien (Ausprägungen). Geprüft werden soll, ob diese überzufällig von einer hypothetischen Verteilung abweicht. Die hypothetische Verteilung kann theoretisch konstruiert oder einer beliebigen Grundgesamtheit entnommen sein.

Die Größe

χ^{2} = \sum_{i = 1}^{I} \frac{{(n_{i} - e_{i})}^{2}}{e_{i}}

folgt einer Chi²-Verteilung mit I-1 Freiheitsgraden. Dabei ist n_i die beobachtete (absolute) Häufigkeit für die i-te Kategorie und e_i die angenommene (erwartete) Häufigkeit für diese Kategorie.

2. Test auf Überzufälligkeit von Zusammenhängen in Kreuztabellen.

Gegeben sei eine Kreuztabelle mit I Zeilen und J Spalten. Es wird folgende Teststatistik berechnet:

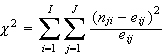
Pearsons Chi-Quadrat-Statistik

Dabei ist n_ij die beobachtete (absolute) Häufigkeit der Zelle in der i-ten Zeile und j-ten Spalte der Tabelle und e_ij die unter der Nullhypothese eines nicht vorhandenen Zusammenhangs erwartete (absolute) Häufigkeit in der entsprechenden Zelle. Es wird also in jeder Zelle die Differenz der beobachteten und erwarteten Häufigkeiten gebildet, das Ergebnis wird quadriert und wiederum durch die erwarteten Häufigkeiten dividiert. Die Werte der einzelnen Zellen werden über alle Spalten und alle Zeilen aufsummiert. Die resultierende Teststatistik, oft auch als Pearsons Chi² bezeichnet, hat (I-1)(J-1) Freiheitsgrade.

Die erwarteten Häufigkeiten werden nach folgender Formel ermittelt:

Hier ist n_i• die absolute Häufigkeit in der i-ten Zeile über alle Spalten (also die Randhäufigkeit der i-ten Zeile), n_•j die absolute Häufigkeit in der j-ten Spalte über alle Zeilen (also die Randhäufigkeit der j-ten Spalte) und n der Gesamtumfang der Stichprobe.

In der Beispielstabelle beim Stichwort Kreuztabelle ergibt sich ein Chi² von 135,58 bei 4 Freiheitsgraden. Der kritische Wert einer Chi-Quadrat-Verteilung mit 4 Freiheitsgraden bei einem Signifikanzniveau von 5 Prozent beträgt 9,49; er wird von der Teststatistik deutlich überschritten. Man wird daher annehmen, dass der beobachtete Zusammenhang auch in der Grundgesamtheit besteht.

Vor allem bei größeren Tabellen (mehr als 2x2 Zellen) wird oft übersehen, dass der Chi²-Test ein »globaler« Test ist; die Teststatistik gibt also nur an, ob sich irgendwelche überzufälligen Zusammenhänge bzw. überzufällig großen Zellhäufigkeiten zeigen oder nicht, sie besagt aber nichts darüber, welche dies sind. In solchen Fällen ist es oft besser, die Zusammenhänge mit einem komplexeren Verfahren zu modellieren, z.B. einem ->log-linearen Modell.

Bei kleineren Stichproben (weniger als 60 Fälle) sollte nach Meinung vieler (aber nicht aller) Autoren ein Chi²-Wert mit sog. Yates-Korrektur verwendet werden. Wenn die erwartete Häufigkeit für wenigstens eine Zelle der Tabelle kleiner 5 ist (nach anderen Autoren: wenn mehr als 20 Prozent der erwarteten Häufigkeiten kleiner 5 sind), ist die Anwendbarkeit des Chi²-Tests nicht mehr gegeben; dann sollten exakte Tests (z.B. nach Fisher) herangezogen werden.

3. Likelihood-Verhältnis-Test

Es sei abschließend noch einmal darauf hingewiesen, dass die Einsatzmöglichkeiten des Chi-Quadrat-Tests bzw. allgemein der Chi-Quadrat-Verteilung wesentlich vielfältiger sind und sich keineswegs auf die genannten drei Möglichkeiten beschränken.