Kruskal-Wallis H-Test

Der H-Test nach Kruskal und Wallis ist ein nichtparametrisches Verfahren zum Vergleich mehrerer Stichproben; er stellt eine Verallgemeinerung von Wilcoxon's Rangsummentest auf mehr als zwei Gruppen dar. Es handelt sich somit um eine Alternative zum F-Test (siehe Varianzanalyse), die vor allem dann angewendet werden sollte, wenn dessen Anwendungsvoraussetzungen verletzt sind, d. h. wenn die Messwerte nicht normalverteilt sind oder die Varianzen der Gruppen stark unterschiedlich sind oder sogar beides gegeben ist.
Voraussetzungen für den H-Test sind lediglich unabhängige Stichproben und mindestens ordinalskalierte Daten.

Zur Berechnung des H-Tests werden die Originaldaten durch die entsprechenden Rangplätze ersetzt, die sich bei der Ordnung der Datenwerte der Größe nach über die Gruppen hinweg ergeben. Im Beispiel sieht das etwa so aus:

Gruppe 1		Gruppe 2		Gruppe 3
Originalwert	Rangplatz	Originalwert	Rangplatz	Originalwert	Rangplatz
1700	1	2100	3	2300	4
2000	2	2400	5	3000	8
2700	6	2800	7	3300	9
3500	10	4400	11	4500	12

Für jede der Gruppen berechnet man dann die Summe der Ränge, die den Messwerten der betreffenden Gruppe zugeordnet sind. Das weitere Verfahren hängt nun von bestimmten Voraussetzungen ab:

1. Sind die untersuchten Stichproben sehr klein (was das bedeutet, ist in der Literatur nicht einheitlich definiert; häufig findet sich: bei drei Gruppen, wenn n<8, bei vier Gruppen, wenn n<4 und bei fünf Gruppen, wenn n<3), muss ein exakter Test durchgeführt werden und die Prüfgröße H mit entsprechenden kritischen Schwellenwerten verglichen werden, die in manchen Statistik-Lehrbüchern tabelliert sind.

2. Sind die untersuchten Stichproben groß genug, d.h. überschreiten sie die unter 1. genannen Grenzen, lässt sich der asymptotische Test durchführen. Die Größe

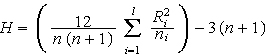
Grafik H-Test

folgt einer Chi²-Verteilung mit l-1 Freiheitsgraden. Dabei ist I die Zahl der Gruppen, R_i sind die Summen der Rangwerte in den einzelnen Gruppen und n_i ist jeweils die Anzahl der Fälle in den betreffenden Gruppen.

Treten Bindungen (engl. »Ties«), d.h. gleiche Werte (und damit gleiche Ränge) über die Gruppen hinweg auf, so wird allen betreffenden Werten das arithmetische Mittel der betreffenden Rangplätze zugewiesen.
Für den Fall, dass es sehr viele Bindungen gibt, steht eine Formel für eine Korrekturgröße zur Verfügung, durch die der Wert der Testgröße dividiert werden sollte und die folgendermaßen berechnet wird:

t_j ist hier die Anzahl der gleichgroßen Werte an der j-ten Stelle. Wenn keine Bindungen vorliegen, nimmt die Korrekturgröße gerade den Wert 1 an.