t-Test (engl.: t-Test)

Ein Verfahren zur statistischen Hypothesenprüfung, bei dem geprüft wird, ob eine Teststatistik im Ablehnungsbereich der T-Verteilung liegt.

Das wichtigste Anwendungsgebiet ist der Vergleich der Mittelwerte zweier Gruppen (Stichproben). Dabei werden zwei Fälle unterschieden:

1. Mittelwertvergleich bei unabhängigen Stichproben

Da die Varianzen der beiden Grundgesamtheiten, aus denen die beiden Stichproben gezogen wurden, meistens unbekannt sind, werden die Varianzen aus der Stichprobe geschätzt. Sind die Varianzen der beiden Untergruppen gleich, so wird folgende Formel herangezogen:

,

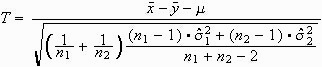andernfalls

.

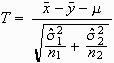Dabei ist
das arithmetische Mittel der ersten Gruppe,
das arithmetische Mittel der zweiten Gruppe,
n₁ der Stichprobenumfang der ersten Gruppe,
n₂ der Stichprobenumfang der zweiten Gruppe,
die Varianz (Schätzwert für die Grundgesamtheit) der ersten Gruppe,
die Varianz (Schätzwert für die Grundgesamtheit) der zweiten Gruppe, und
eine Größe, deren Betrag der zu prüfenden Nullhypothese entspricht. Diese Größe wird meist gleich Null gesetzt, d. h., es wird geprüft, ob die Differenz der beiden Mittelwerte größer als Null ist.

Die Teststatistik T folgt einer t-Verteilung mit k Freiheitsgraden. Im Falle gleicher Varianzen hat k den Betrag n₁ + n₂ - 2. Bei ungleichen Varianzen wird k geschätzt durch die Welch-Satterthwaite-Approximation (das Ergebnis ist gegebenenfalls auf die nächste ganze Zahl zu runden):

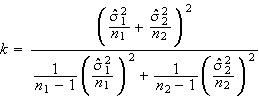
Die Gleichheit der beiden Varianzen kann z. B. durch den Levene-Test geprüft werden. Wird die Nullhypothese der Varianzgleichheit nicht abgelehnt, so ist die erste der oben angeführten Formeln für den t-Test zu verwenden, andernfalls die zweite.

Hinweis: Sind die Varianzen der Grundgesamtheiten bekannt, aus denen die beiden Gruppen stammen, so ist die Teststatistik

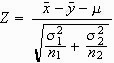
normalverteilt.

2. Mittelwertvergleich bei abhängigen (oder verbundenen) Stichproben

Dieser Fall liegt z.B. vor, wenn bei den Untersuchungseinheiten einer Stichprobe ein Merkmal zweimal gemessen und geprüft wird, ob der zweite Messwert höher (oder niedriger) als der erste liegt, oder wenn bei Ehepaaren untersucht wird, ob die Einkommen der Frauen unter denen der Männer liegen (bzw. ob die Differenz einen Betrag überschreitet). Die T-Statistik wird hier berechnet als

,

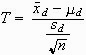mit
als dem arithmetischen Mittel der Differenzen der Messwerte der einzelnen Paare, und
als der Standardabweichung dieser Differenzen, die gemäß der Formel

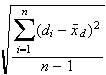
berechnet wird. (d_i sind hier die Differenzen der Messwerte der einzelnen Paare.)

Die Größe T folgt einer t-Verteilung mit n-1 Freiheitsgraden; n ist hier die Anzahl der Messwertpaare (also nicht der einzelnen Messungen!).

Anwendungsvoraussetzungen: Der t-Test kann eingesetzt werden, wenn die zu untersuchende abhängige Variable mindestens (mehr oder weniger) intervallskaliert ist (siehe Messniveau). Außerdem sollte das Merkmal in den untersuchten Populationen normalverteilt sein; vor allem bei großen Stichproben und nicht zu unterschiedlichem Umfang der beiden Gruppen ist das Verfahren jedoch relativ robust gegen die Verletzung dieser Annahme. Eine genauere Diskussion findet sich bei Bortz bzw. Bortz/Schuster (2010).

Literatur:

• Bortz, Jürgen/Schuster, Christof: Statistik für Human- und Sozialwissenschaftler, 7., vollständig überarbeitete und aktualisierte Auflage. Berlin, Heidelberg, New York: Springer, 2010.
  Frühere Auflagen in Alleinautorenschaft von Jürgen Bortz, teilweise unter dem Titel »Statistik für Sozialwissenschaftler« bzw. »Lehrbuch der Statistik für Sozialwissenschaftler«

© W. Ludwig-Mayerhofer, ILMES | Last update: 11 Nov 2010