Multinomiales Logit-Modell (engl.: Multinomial Logit Model)
Das M. L.-M. stellt eine Erweiterung des Verfahrens der binären logistischen Regression auf eine kategoriale abhängige Variable mit mehr als zwei Ausprägungen dar. Die Ausprägungen werden nicht als geordnet, sondern als Kategorien einer nominalskalierten Variablen interpretiert.
Als Ausgangspunkt können auch hier die Odds zwischen zwei Ausprägungen des untersuchten Merkmals fungieren. Bezeichen wir die Zahl der Ausprägungen mit I, so können insgesamt I-1 nicht-redundante Odds berechnet werden:
![]()
![]()
usw. bis
![]()
Die übrigen Odds lassen sich hieraus berechnen, z.B.
![]()
Für die Logits gilt entsprechend
![]()
usw. Die redundanten Logits ergeben sich in Analogie zu den Odds, beispielsweise als
![]()
Entsprechend werden (simultan) I-1 Regressionsmodelle geschätzt:
![]()
![]()
usw. bis
![]()
Es werden also I-1 Gleichungen mit jeweils spezifischen Regressionsgewichten geschätzt, weswegen multinomiale Logit-Modell u.U. sehr komplex werden können.
Für die übrigen Logits (i ≠ j, j ≠ I) ergibt sich in Analogie zu oben:
![]()
Die Gleichungen lassen sich wiederum durch Bildung des Antilogarithmus in Odds übersetzen:
![]()
usw.
Die Effekte auf die Wahrscheinlichkeiten der einzelnen Ausprägungen lassen sich nach
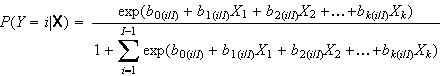
(mit i = 1, 2, ... I-1) berechnen; für die letzte (I-te) Kategorie lautet die Gleichung
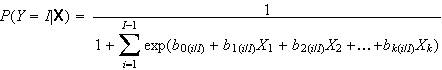
Die Regressionsparameter werden auf der Grundlage des Maximum Likelihood-Verfahrens geschätzt. Inferenzstatistische Verfahren stehen sowohl für die einzelnen Regressionskoeffizienten als auch für das Gesamtmodell zur Verfügung (siehe Wald-Statistik und Likelihood-Verhältnis-Test); in Analogie zum linearen Regressionsmodell wurden auch Verfahren der Regressionsdiagnostik entwickelt, anhand derer einzelne Fälle mit übergroßem Einfluss auf das Ergebnis der Modellschätzung identifiziert werden können (solche Verfahren sind leider in kaum einem Statistik-Paket implementiert). Schließlich gibt es auch einige Vorschläge zur Berechnung einer Größe, die in Analogie zum R2 der linearen Regression eine Abschätzung der »erklärten Varianz« erlaubt; man spricht hier von sog. Pseudo-R2. Auch das AIC und das BIC werden in diesem Kontext gelegentlich herangezogen.
Bei multinomialen Logit ist zu beachten, dass die Richtung der Wirkungen einer Variablen auf die Logits (und damit die Odds) nichts über die Wirkung auf die Wahrscheinlichkeiten aussagt. Betrachten wir dazu folgendes Beispiel (die Daten stammen aus dem Buch von Andreß/Hagenaars/Kühnel (1997) und wurden für das Beispiel so modifiziert, dass die F.D.P. nunmehr die letzte, d.h. I-te Kategorie darstellt):
| Ohne Bindung | Mit Bindung | |
|---|---|---|
| SPD | 41,3% | 35,4% |
| CDU | 29,8% | 56,9% |
| F.D.P | 28,9% | 7,7% |
| N | 346 | 404 |
Ein typisches Statistik-Paket bringt nun folgenden Output (B = Regressionskoeffizient, S.E. = Standardfehler des Koeffizienten [von engl. »Standard Error«]):
| Effekt | B | S.E. | Exp(B) |
|---|---|---|---|
| Konstante | 0,358 | ||
| Konf. Bindung: | 1,171 | 0,237 | 3,226 |
| Effekt | B | S.E. | Exp(B) |
|---|---|---|---|
| Konstante | 0,030 | ||
| Konf. Bindung: | 1,975 | 0,237 | 7,203 |
Diese Ergebnisse sind völlig korrekt: Sie besagen, dass die Odds der SPD gegenüber der F.D.P. für Personen mit konfessioneller Bindung im Vergleich zu Personen ohne Bindung um einen Faktor von mehr als 3 zunehmen. Was jedoch nicht zu sehen ist (aber dennoch vielfach so interpretiert wird), ist die Tatsache, dass die Wahrscheinlichkeit einer Präferenz für die SPD bei konfessioneller Bindung abnimmt. Der Grund für diese diskrepanten Ergebnisse ist offenkundig: Da die Wahrscheinlichkeit einer Präferenz für die F.D.P. bei konfessioneller Bindung noch viel drastischer abnimmt als die einer Präferenz für die SPD, kann das Logit SPD/F.D.P. einen positiven Wert annehmen.
Für eine korrekte Interpretation der Ergebnisse ist es also sinnvoll, die direkten Effekte einzelner Variablen auf die Wahrscheinlichkeiten zu berechnen; dabei ist zu beachten, dass diese Effekte jeweils von der Konstellation der übrigen Variablen abhängen.
Literatur:
- Agresti, Alan: Categorical Data Analysis. New York: Wiley, 1990, 2. Auflage 2002, 3. Auflage 2015
- Andreß, Hans-Jürgen/Hagenaars, J.-A./Kühnel, Steffen: Analyse von Tabellen und kategorialen Daten. Berlin u.a.: Springer, 1997
© W. Ludwig-Mayerhofer, ILMES | Last update: 18 July 2004