Tau-a, Tau-b, Tau-c
Bei den Koeffizienten Tau-a, Tau-b, Tau-c handelt es sich um drei Varianten eines Zusammenhangsmaßes, das vorrangig für ordinalskalierte Daten verwendet wird. Diese Koeffizienten sollten nicht verwechselt werden mit Goodman und Kruskals Tau, welches ein Zusammenhangsmaß für nominalskalierte Daten darstellt.
Bevor ich die allgemeine Logik dieser Koeffizienten erkläre, hier ganz kurz Hinweise zum Gebrauch: Der Koeffizient Tau-a ist nur sinnvoll, wenn es keine »Ties« oder »gebundenen Paare« gibt (zur Erläuterung siehe unten). Da das in sozialwissenschaftlichen Anwendungen praktisch nie vorkommt, werden vorrangig die anderen beiden Maße eingesetzt: Tau-b kann am besten verwendet werden, wenn die Zahl der Ausprägungen der beiden Variablen gleich ist (in einer Kreuztabelle ausgedrückt: wenn die Zahl der Zeilen und der Spalten der Tabelle gleich groß ist). Ist das nicht der Fall, so kann Tau-b nicht den Maximalwert von |1| erreichen. Tau-c soll hier Abhilfe schaffen; der Koeffizient wird aber generell als wenig befriedigend empfunden, so dass sich in der Praxis Tau-b als der am meisten verwendete Koeffizient durchgesetzt hat.
Die Berechnung dieser Maße ist leider etwas umständlich (sie wird üblicherweise an geeignete Statistik-Software delegiert). Wir versuchen eine Erläuterung anhand eines Beispiels Dazu verwenden wir eine ganz einfache fiktive Tabelle. Sie ist angelehnt an einen Befund von Stefan Liebig und Jürgen Schupp (Leistungs- oder Bedarfsgerechtigkeit? Über einen normativen Zielkonflikt des Wohlfahrtsstaats und seiner Bedeutung für die Bewertung des eigenen Erwerbseinkommens, Soziale Welt, Bd. 59 (1) 2008, S. 7-30) zur wahrgenommenen (Un-)Gerechtigkeit des eigenen Erwerbseinkommens in Ost- und Westdeutschland; die hier dargestellten Zahlen sind aber aus Gründen der Vereinfachung frei erfunden. Die Variablen sind binär, können aber (gerade deshalb) als ordinal aufgefasst werden (Westdeutsche sind westdeutscher als Ostdeutsche oder umgekehrt).
| Ost | West | ALLE | |
|---|---|---|---|
| Ungerecht | 60 | 30 | 90 |
| Gerecht | 40 | 70 | 110 |
| N | 100 | 100 | 200 |
Die allgemeine Logik der Koeffizienten beruht darauf, sämtliche Untersuchungseinheiten miteinander zu vergleichen; d.h., jede Einheit wird mit jeder anderen verglichen. Daher ist im folgenden oft von Paaren die Rede. Zunächst werden nun einige Begriffe definiert:
Unter einem konkordanten Paar versteht man ein Paar von Untersuchungseinheiten mit folgender Konstellation: Diejenige Person, die in der einen Variablen den kleineren Wert , hat auch in der anderen Variablen den kleineren Wert. In unserem Beispiel gelten »ungerecht« und »ostdeutsch« als die kleineren Werte. Es gibt also 60 Personen, die in beiden Variablen den kleineren Wert haben, und 70 Personen, die in beiden Variablen den größeren Wert haben. Das heißt: Zu jeder der 60 Personen, die in beiden Variablen den kleineren Wert haben, gibt es 70 ›Vergleichsobjekte‹, die in beiden Variablen den größeren Wert haben, es gibt also 60 * 70 = 4.200 konkordante Paare.
Unter einem diskordanten Paar versteht man das Gegenteil, also ein Paar von Untersuchungseinheiten mit folgender Konstellation: Diejenige Person, die in der einen Variablen den kleineren Wer hat, hat in der anderen Variablen den größeren Wert. Es gibt 30 Personen, die in der Variablen »Wohnort« den größeren, aber in der Variablen »Gerechtigkeit« den kleineren Wert haben, und dazu 40 Personen, bei denen es genau umgekehrt ist. Es gibt also 30 * 40 = 1.200 diskordante Paare.
Nun gibt es noch eine Reihe von Paaren, die weder konkordant noch diskordant sind. So können wir etwa die ostdeutschen oder die westdeutschen Personen untereinander vergleichen. Wir können sagen: Es gibt zu jeder der 60 ostdeutschen Personen, die ihr Einkommen als ungerecht empfinden, 40 Vergleichsobjekte, die zwar in der Variablen »Wohnort« den gleichen Wert haben, aber in der Variablen »Gerechtigkeit« einen anderen Wert (selbstverständlich könnte man das ganze auch umgekehrt aus der Perspektive der Personen mit als gerecht empfundenem Lohn betrachten, im Ergebnis ist das aber das gleiche.) Solche Paare, die in einer Variablen den gleichen, aber in der anderen verschiedene Werte haben, nennt man »gebundene« oder »verknüpfte« Paare, auf englisch »Ties«. Neben den 60 * 40 = 2.400 gebundenen Paaren in der Spalte »Ostdeutschland « gibt es auch noch 30 * 70 = 2.100 Ties in der Spalte »Westdeutschland«; insgesamt also 4.500 Ties in der Spaltenvariablen.
Das gleiche kann man nun noch aus der Sicht der Zeilenvariablen machen: Die 90 Personen mit als ungerecht wahrgenommenem Einkommen (also niedrigerer Wert in der Zeilenvariablen) teilen sich ein in 60 Personen, die auch in der Spaltenvariablen den niedrigeren Wert haben, und 30 Personen mit einem anderen Wert. Es ergeben sich also in der ersten Zeile 60 * 30 = 1.800 Ties, in der zweiten Zeile 40 * 70 = 2.800 Ties, insgesamt also 4.600 Ties in der Zeilenvariablen.
Eine Gruppe von Ties fehlt jetzt noch: Fälle, die in beiden Variablen den gleichen Wert haben - also die 60 Fälle in der Zelle links oben, die 30 Fälle in der Zelle rechts oben sowie die analogen 40 bzw. 70 Fälle in der unteren Zeile. Weil sich die hieraus ergebenden Vergleiche aber notwendigerweise auch als Rest aus der Summe aller möglichen Vergleiche minus den bislang genannten Konstellationen ergeben, brauchen wir zum Glück hierauf nicht weiter einzugehen.
Nun benötigen wir noch Abkürzungen, um die Formeln darzustellen. Wir bezeichen mit
Nc die Zahl der konkordanten Paare (Number of concordant pairs);
Nd die Zahl der diskordanten Paare (Number of discordant pairs);
Tx die Zahl der Ties in der Spaltenvariablen (Ties in x; x steht hier für die Spaltenvariable );
Ty die Zahl der Ties in der Zeilenvariablen (Ties in y; y steht hier für die Zeilenvariable );
Die Formeln für die einzelnen Koeffizienten lauten nun:
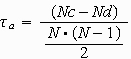
Dabei steht N für die Gesamtzahl der Fälle; der Ausdruck im Nenner ist die Gesamtzahl aller möglichen Paare. Man erkennt, dass in dieser Formel die Ties nicht auftauchen, weswegen sie im vorliegenden Fall nicht anwendbar ist.
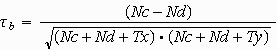
In unserem Fall ergibt sich ein Wert von 0,30151.
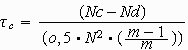
Dabei steht m für die Zahl der Zeilen, wenn die Tabelle weniger Zeilen als Spalten hat, und im umgekehrten Fall für die Zahl der Spalten. (Tau-c ist just für den Fall gedacht, dass die beiden Werte sich unterscheiden.) In unserem Fall ergibt sich ein Wert von 0,30.
Gemeinsam ist allen Formeln, dass im Zähler die Zahl der diskordanten Paare von der der konkordanten Paare abgezogen wird. Daraus ergibt sich (wie es auch gewünscht wird), dass der Wert der Koeffizienten bei einem positiven Zusammenhang der Variablen (es gibt viele Fälle, wo große bzw. kleine Werte in beiden Variablen gemeinsam auftreten) einen positiven Betrag hat, im umgekehrten Fall dagegen einen negativen Betrag.
In der Beispielstabelle beim Stichwort Kreuztabelle liegen die Dinge um einiges komplizierter. Ich will hier nur die Berechnung der konkordanten Paare verdeutlichen: Die 3.469 Fälle, welche niemals arbeitslos und niemals arm waren, können in Beziehung gesetzt werden mit den 208 + 90 + 34 + 28 Fällen, welche sowohl in der Variablen »Arbeitslosigkeit« als auch in der Variablen »Armut « einen größeren Wert haben (1.248.840 konkordante Paare, wenn ich mich nicht verrechnet habe). Ebenfalls konkordante Paare ergeben sich noch für den Vergleich der 563 Fälle, die bei einem Jahr Arbeitslosigkeit niemals arm waren, mit den 90 + 34 + 28 Fällen, die sozusagen rechts unterhalb liegen, sowie schließlich aus dem entsprechenden Vergleich der 152 Fälle mit 2 Jahren und den 55 Fällen mit 3 Jahren Arbeitslosigkeit. Der Wert von Tau-b beträgt (gerundet) 0,15, der von Tau-c 0,10.
Zur inferenzstatistischen Prüfung, ob die vorgefundenen Zusammenhänge überzufällig sind, können die Tau-Koeffizienten durch ihre Standardfehler dividiert werden (die Standardfehler werden von Statistik-Software i. d. R. zusammen mit den Koeffizienten ausgegeben). Beträgt der Wert der Koeffizienten mindestens das 1,96-fache ihres Standardfehlers, so kann – hinreichend große Fallzahlen vorausgesetzt – die Nullhypothese, dass es sich um einen zufällig gefundenen Zusammenhang handelt, bei einem Signifikanzniveau von 5 Prozent verworfen werden. Es sollte also zur Prüfung der Signifikanz nicht der Chi²-Test für die Kreuztabelle herangezogen werden, da dieser der unterstellten ordinalen Natur des Zusammenhangs nicht gerecht wird.
Neben den hier behandelten Koeffizienten spielen noch einige andere eine Rolle (siehe unten). Dennoch kann man sagen, dass sich – bei manchen Vorbehalten – Tau-b als der am besten geeignete Koffizient in der Praxis am ehesten durchgesetzt hat.
Siehe auch: Gamma; Somers' D; Spearmans Rho.
© W. Ludwig-Mayerhofer, ILMES | Last update: 6 Aug 2025