Verweildaueranalyse, auch: Verlaufsdatenanalyse, Ereignisanalyse, Survival-Analyse (engl.: Survival Analysis, Analysis of Failure Times, Event History Analysis)

In der Verweildaueranalyse wird untersucht, wie lange Untersuchungseinheiten in einem (Ausgangs-)Zustand bleiben. Typische Fragestellungen sind: Wie lange dauern Ehen? Wie lange dauert es, bis eine arbeitslose Person wieder einen Job gefunden hat? Wie lange dauert es, bis nach einer Behandlung eine erneute Erkrankung auftritt? Wie lange dauert es, bis eine PC-Festplatte kaputt geht? Bei diesen und zahllosen denkbaren weiteren Fragestellungen wird es ferner häufig darum gehen, den Einfluss erklärender Variablen (Kovariaten) auf die untersuchte Verweildauer zu erforschen.

Obwohl es sich bei Verweildauern im Allg. um metrische Variablen handelt, können diese zumeist nicht mit den üblichen Verfahren der Regressionsanalyse untersucht werden. Neben der Beobachtung, dass viele Verweildauern nicht normalverteilt sind, ist vor allem von Bedeutung, dass meist nicht von allen Untersuchungseinheiten einer Stichprobe die Verweildauer im Ausgangszustand bekannt ist. Dies liegt entweder an begrenzten Beobachtungszeiträumen oder – fast noch häufiger – daran, dass nicht bei allen Untersuchungseinheiten das Ereignis des Übergangs in einen anderen Zustand auftritt (nicht alle Ehen werden geschieden, nicht alle Arbeitslosigkeitsepisoden enden mit einem Übergang in einen neuen Job). Man spricht in diesem Fall von rechtszensierten Daten. Linkszensierte Daten liegen dagegen vor, wenn nicht bekannt ist, seit wann der Ausgangszustand vorliegt (wann also die Ehe, die Arbeitslosigkeit, die Behandlung begonnen hat). Während linkszensierte Daten nur sehr begrenzt analysiert werden können, können rechtszensierte Daten mit modernen Verfahren der statistischen Datenanalyse sehr gut ausgewertet werden. Eine Voraussetzung hierfür ist allerdings, dass die Zensierungen nicht mit dem untersuchten Prozess kausal zusammenhängen. (Beispiel: Wenn eine Behandlung dazu führt, dass Personen misstrauisch gegenüber den Therapeuten werden und die Behandlung deshalb abbrechen – und so als zensiert erscheinen –, dann dürfte die Annahme der Unabhängigkeit von Zensierung und untersuchtem Prozess verletzt sein).

Grundbegriffe

Im Falle stetiger Zeit (d.h.: annähernd stetig gemessener Zeit!) ist die Dichtefunktion der Verweildauern als die Wahrscheinlichkeit eines Übergangs in den Zielzustand (eines »Ereignisses«) in einem infinitesimal klein werdenden Zeitintervall definiert:

Hieraus ergibt sich folgende Verteilungsfunktion der Verweildauern:

Diese gibt also an, wie viele Dauern kleiner oder gleich einem Wert t sind. Häufiger wird jedoch die Gegenfunktion, die Survivorfunktion

herangezogen; diese gibt die Wahrscheinlichkeit an, dass der Übergang in den Zielzustand nach t liegt, anders gesagt, wie groß der Anteil der Untersuchungseinheiten ist, die den Zeitpunkt t ›überleben‹.

Als entscheidende theoretische Größe, die vor allem in der Modellierung von Prozessen als zentrale abhängige Variable fungiert, ist schließlich die Hazardrate

zu sehen. Diese kann verstanden werden als die momentane Neigung zum Zustandswechsel unter jenen Untersuchungseinheiten, die bis zum Zeitpunkt t noch keinen Zustandswechsel erfahren haben.

In manchen Verfahren spielt schließlich die kumulative Hazardrate

eine Rolle.

Alle genannten Größen lassen sich in analoger Weise für diskrete Zeit definieren.

Zurück zum Seitenbeginn

Nicht-parametrische Verfahren

Life-Table-Schätzer

Beim Life-Table-Schätzer wird die Prozesszeit in Intervalle eingeteilt; errechnet werden die Survivorfunktionen zu Beginn des jeweiligen Intervalls (im Programm SPSS: zu Ende des Intervalls) sowie für jedes Intervall die Dichte- und Hazardfunktion (und deren Standardfehler).

Benennen wir die Zahl der Fälle, die im jeweiligen Intervall ein Ereignis (Übergang in den Zielzustand) erfahren, mit E_l und die Zahl der Fälle mit Zensierungen in einem Intervall mit Z_l, so lässt sich zunächst die Risikomenge – die Zahl der Fälle, die im jeweiligen Intervall dem Risiko eines Ereignisses unterliegt – berechnen. Hier wird wiederum die Zahl der Fälle benötigt, die zu Beginn eines Intervalls noch nicht ausgeschieden ist (durch ein Ereignis oder durch Zensierung). Diese ist für das erste Intervall gleich N (der Gesamtzahl der Fälle), für alle folgenden Intervalle gilt:

Zur Berechnung der Risikomenge sind nun Annahmen über die Verteilung der zensierten Fälle während des Intervalls zu machen. Üblicherweise wird angenommen, dass die Zensierungen gleichmäßig über das gesamte Intervall verteilt sind; daraus folgt, dass die Zahl der Fälle zu Beginn des Intervalls um die Hälfte der Zensierungen während dieses Intervalls zu reduzieren ist, um die Risikomenge zu erhalten. Die Risikomenge R wird also folgendermaßen bestimmt:

Die bedingte Wahrscheinlichkeit eines Ereignisses in einem Intervall ist definiert als

und dementsprechend ist die (bedingte) Wahrscheinlichkeit, in dem Intervall kein Ereignis zu haben (also das Intervall zu überleben)

Für die Survivorfunktion ergibt sich:

Die Dichtefunktion ist dann

mit h_l als der Breite des Intervalls, und die Hazardrate wird berechnet als

mit

ist also gewissermaßen die ›durchschnittliche‹ Survivorfunktion während des Intervalls.

Kaplan-Meier-Schätzer (auch: Produkt-Limit-Schätzer)

Dieser Schätzer beruht auf exakten Zeiten (also nicht: gruppierten, wie beim Life-Table-Schätzer). Die Survivorfunktion ist definiert zu Zeitpunkten, zu denen Ereignisse eintreten. q_l und p_l lassen sich wie beim Life Table-Schätzer definieren. Im Gegensatz zu letzerem wird hier unterstellt, dass Zensierungen – sofern sie im Datensatz zur der gleichen Zeit auftreten wie Ereignisse – in Wahrheit ›kurz nach&lsaquot den Ereignissen eingetreten sind. Daher ist die Risikomenge identisch mit der Zahl der Fälle zum jeweiligen Zeitpunkt, in der obigen Terminologie gilt also R_l und N_l. Die Survivorfunktion wird dann geschätzt als Produkt der Überlebenswahrscheinlichkeiten:

Da die Survivorfunktion hier nur zu (vielen) Zeitpunkten definiert ist, lassen sich f(t)und r(t) nicht berechnen.

Nicht-parametrische Tests zur Überprüfung von Unterschieden zwischen Überlebensdauern auf statistische Signifikanz

Es liegen mehrere nicht-parametrische Tests vor, mit denen zwei oder mehr Gruppen auf statistisch signifikante Unterschiede in der Überlebensdauer geprüft werden können. Die wichtigsten dieser Tests sind: der Log-Rank-Test (Mantel 1966), der generalisierte Wilcoxon-Test nach Breslow (1970) und Gehan (1965), der Tarone-Ware-Test (Tarone & Ware 1977) und ein Test von Peto & Peto (1972) bzw. Prentice (1978).

Zurück zum Seitenbeginn

Ein semi-parametrisches Verfahren: Die Cox-Regression (auch: Partial-Likelihood-Verfahren)

Zu diesem Verfahren gibt es einen eigenen Lexikon-Eintrag.

Zurück zum Seitenbeginn

Parametrische Verfahren

In der Literatur findet sich eine Vielzahl parametrischer Regressionsmodelle für Verlaufsdaten. Im folgenden werden nur einige wichtige (häufige) Verfahren dargestellt.

Modelle mit über die Zeit konstanter Rate

Für stetige Zeit ist hier das Exponentialmodell einschlägig:

Für diskrete (oder diskret gemessene) Zeit gibt es Verfahren, die sich an die logistische Regression anlehnen:

Modelle mit zeitveränderlicher Rate

Zeitverändliche Raten können im wesentlichen auf drei Wegen modelliert werden:

durch Aufnahme von Polynom-Termen für die Zeit,

durch Modellierung perioden- oder zeitabschnitts-spezifischer Regressionskonstanten (gegebenenfalls auch periodenspezifischer Einflüsse),

durch Wahl einer geeigneten Verteilung für die Hazardrate.

Nur der erste Weg ist sowohl für stetige als auch für diskrete Verweildauern möglich. Alle übrigen Verfahren sind nur für stetige Zeit ausformuliert.

Modelle mit Polynom-Termen für die Zeit

Exponential-Modell mit Polynom-Term

Dieses Modell (für stetige Dauern) liegt in mehreren Formulierungen vor. Ich wähle diejenige, die, soweit ich beurteilen kann, am brauchbarsten ist:

Bei den hier mit d_r bezeichneten Parametern handelt es sich also um »Regressionsgewichte«, mit denen die Dauer t bzw. Vielfache derselben gewichtet werden. Der Grad des Polynoms muss vom Nutzer nach theoretischen oder empirischen Gesichtspunkten festgelegt werden.

Logistisches Regressionsmodell mit Polynom-Term

Hierbei handelt es sich um das Äquivalent zum Exponentialmodell (die d_r sind daher ganz analog zu verstehen):

Modelle mit periodenspezifischen Konstanten bzw. Einflüssen

Das Piecewise-Constant-Exponential-Modell:

In diesem Modell werden verschiedene intervallspezifische Konstanten geschätzt. Es gilt also:

wobei das Subskript l anzeigt, dass für beliebige – vom Nutzer anzugebende – Intervalle l jeweils eine spezifische Konstante geschätzt wird, die die »Basishöhe« der Hazardrate in diesem Intervall angibt.

Modelle mit periodenspezifischen Effekten:

Hier wird nicht nur für jedes Intervall l eine unterschiedliche Regressionskonstante geschätzt; auch die Regressionsgewichte werden intervallspezifisch bestimmt:

Modelle mit speziellen Verteilungen für die Hazardrate

Hier besteht zweifelsohne die größte Bandbreite; im Folgenden können nur einige wenige bekannte Modelle vorgestellt werden. Viele Modelle enthalten sog. »Hilfsparameter« (meist als a bezeichnet), die sich im Allgemeinen auf die Form der Hazardrate auswirken (in vielen Modellen heißen sie daher auch »Shape-Parameter«). Diese Hilfsparameter werden im allgemeinen als Konstante geschätzt; ein Spezialprogramm für Verlaufsdaten (TDA) erlaubt auch die Modellierung von Kovariaten-Einflüssen auf diese Hilfsparameter. Hierauf wird hier aber nicht weiter eingegangen.

Das Weibull-Modell:

In diesem Modell kann die Hazardrate monoton fallen oder steigen. Die Hazardrate wird folgendermaßen modelliert:

Ist a < 1, so liegt eine sinkende Hazardrate vor, ist a >1, steigt die Rate. (Viele Programme schätzen ln(a); eine sinkende Rate liegt also bei ln(a) < 0, eine steigende Hazardrate bei ln(a) > 0 vor.)

Das log-logistische Modell:

Mit diesem Modell kann eine fallende oder eine zunächst steigende und dann fallende Hazardrate modelliert werden. Die Formel für die Rate lautet hier:

Ist a < 1, so liegt eine sinkende Hazardrate vor, ist a >1, steigt die Rate zunächst und sinkt dann. (Viele Programme schätzen ln(a); eine sinkende Rate liegt also bei ln(a) < 0, eine zunächst steigende und dann sinkende Hazardrate bei ln(a) > 0 vor.)

Diesem Modell kann man auch eine inhaltliche Interpretation geben : Aus den Parametern lassen sich das Maximum der Hazardrate (r_max) und auch der Zeitpunkt, zu dem dieses Maximum erreicht wird (t_max), berechnen (natürlich in Abhängigkeit von gegebenen Ausprägungen der Kovariaten):

Das Log-Normal-Modell

Die Formel für die Hazardrate in diesem Modell lautet:

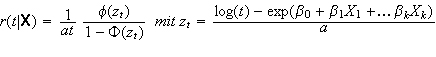
Lognormales Ratenmodell

Dabei steht φ für die Dichtefunktion der Standardnormalverteilung

und für die Verteilungsfunktion

Das Log-Normal-Modell unterstellt eine zunächst steigende und dann fallende Hazardrate.

Das Sichel-Modell

Auch dieses Modell kann zunächst steigende und dann fallende Raten modellieren, die der Form einer Sichel ähneln:

Das Maximum der Rate liegt bei t=a und der (einzige) Wendepunkt bei t=2a.

Eine Besonderheit dieses Modells ist, dass die Survivorfunktion nicht gegen 0 tendiert, sondern gegen

Mit anderen Worten, dieses Modell ist vor allem dann angemessen, wenn man annimmt, dass nicht alle Personen ein Ereignis haben; daher ist es z.B. für die Analyse von Ehescheidungen gut geeignet.

Zurück zum Seitenbeginn

Competing Risks (konkurrierende Risiken)

Nicht selten gibt es für einen Ausgangszustand mehrere Zielzustände: Ein Arbeitsloser kann in eine Beschäftigung, aber auch in Ausbildung übergehen oder sich ganz aus dem Arbeitsmarkt zurückziehen, ein Kranker kann an der Krankheit sterben, deretwegen er behandelt wurde, aber auch an einer anderen Krankheit oder aus anderen Ursachen sterben.

In allen diesen Fällen spricht man von »konkurrierenden Risiken« oder Competing Risks. Sofern diese voneinander unabhängig sind, ist ihre statistische Behandlung einfach: Bei der Untersuchung der Übergänge in einen bestimmten Zielzustand werden alle anderen Übergänge als Zensierungen behalten, also als Beendigung der Beobachtungsdauer, ohne dass das untersuchte Zielereignis eingetreten wäre. Sind die verschiedenen Zielzustände jedoch nicht unabhängig (z.B.: Arbeitslose entscheiden sich umso mehr für eine Weiterbildung, je länger sie keinen Job gefunden haben), ist dieses Verfahren nicht zulässig. Eine adäqute statistische Behandlung solcher abhängiger Risiken ist m.W. noch nicht möglich.

Zurück zum Seitenbeginn

Episodensplitting (zeitveränderliche Kovariaten)

Ein Vorzug der Verlaufsdatenanalyse ist, dass auch solche unabhängige Variablen untersucht werden können, deren Werte sich im Zeitverlauf selbst ändern (z.B. Zahl der Kinder, der Bildungsstand oder auch Kontextmerkmale wie die regionale Arbeitslosenquote). Im Modell der Cox-Regression sind Prozeduren implementiert, wie solche Variablen analysiert werden können. Will man andere Modelle verwenden, so greift man zum Verfahren des Episodensplitting.

Beim Episodensplitting wird eine Episode immer dann, wenn eine zeitveränderliche Kovariate ihren Wert ändert, »gesplittet«. Dabei geht man so vor, dass das Ende der ersten (Teil-)Episode zu dem Zeitpunkt angesetzt wird, an dem die Veränderung in der Kovariaten eintritt; die Folgeepisode beginnt zu genau diesem Zeitpunkt. Die erste Teilepisode muss natürlich als zensiert betrachtet werden (wäre zum Zeitpunkt der Änderung der Kovariaten ein Übergang in den Zielzustand aufgetreten, wäre diese Änderung gar nicht mehr für den untersuchten Prozess relevant). Episoden lassen sich beliebig oft auch bei Änderungen mehrerer Kovariaten splitten.

Beispiel:

Nehmen wir an, wir untersuchen die Beschäftigungsdauer von Personen. Frauen unterbrechen in Deutschland ihre Erwerbstätigkeit vor allem dann, wenn sie Kinder bekommen, es könnte jedoch auch untersucht werden, ob eine Heirat zu einer Erwerbsunterbrechung führt (das war früher häufiger der Fall.) Nehmen wir an, eine Person heiratet 37 Monate nach Eintritt in die Erwerbstätigkeit, bekommt 43 Monate nach diesem Eintritt ihr erstes und 73 Monate nach dem Eintritt ihr zweites Kind. Nach 85 Monaten lässt sie sich scheiden und nach 98 Monaten beendet sie ihre Beschäftigung. Der Datensatz muss dann folgende Variablen enthalten: Beginn der (Teil-)Episode, Ende der Teilepisode, Angabe, ob die Episode mit einem Ereignis endete (1=ja, 0=nein), den Ehestatus (1=verheiratet, 0=nicht verheiratet) und die Zahl der Kinder. Die Daten für diese Person sähen dann folgendermaßen aus:

Beginn	Ende	Ereignis?	Ehestatus	Kinder
0	37	0	0	0
37	43	0	1	0
43	73	0	1	1
73	85	0	1	2
85	98	1	0	2

Zu beachten ist, dass keineswegs alle Software-Pakete mit dieser Datenstruktur umgehen können. Hierfür ist es erforderlich, die Anfangszeit der Episode explizit angeben zu können, während viele Statistikprogramme diese Anfangszeit durchgängig als Null setzen.

Zitierte Literatur:

Breslow, N.: A generalized Kruskal-Wallis test for comparing K samples subject to unequal patterns of censorship, in: Biometrika 57, 1970, S. 579-594
Gehan, Edmund A.: A generalized Wilcoxon test for comparing arbitrarily singly censored samples, in: Biometrika 52, 1965, S. 203-223
Mantel, N.: Evaluation of survival data and two new rank order statistics arising in its consideration, in: Cancer Chemotherapy Reports 50, 1966, S. 163-170
Peto, Richard/Peto, Julian: Asymptotically efficient rank invariant test procedures, in: Journal of the Royal Statistical Society A 135, 1972, S. 185-206
Prentice, R. L.: Linear rank tests with right censored data, in: Biometrika 65, 1978, S. 167-179
Tarone, R. E./Ware, J.: On distribution-free tests for equality of survival distributions, in: Biometrika 64, 1977, S. 156-160

Weitere Literatur:

Box-Steffensmeier, Janet M./Jones, Bradford S.: Event History Modeling: A Guide for Social Scientists. Cambridge: Cambridge University Press, 2004