Spearmans Korrelationskoeffizient, Spearmans Rho (engl.: Spearman's rank correlation coefficient)

S. K. ist ein Zusammenhangsmaß für metrisch skalierte Merkmale (siehe Messniveau), mit dem sich der monotone Zusammenhang zwischen zwei Variablen bestimmen lässt. Da der Koeffizient jedoch nur die Ordnungsrelation der Werte benutzt, kann er bereits bei Merkmalen, die auf Ordinalskalenniveau gemessen sind, angewendet werden. Im Gegensatz zum Bravais-Pearson-Korrelationskoeffizienten wird r_SP zudem weniger stark von Ausreißern beeinflusst.

Zur Berechnung dieses Koeffizienten wird von den urpsrünglichen Werten der Variablen X und Y zu Rängen übergegangen, d.h. jedem x-Wert und jedem y-Wert wird als Rang die Platzzahl zugeordnet, die der Wert nach Anordnung aller x- und y-Werte der Größe nach erhält. Aus den ursprünglichen Messpaaren (x_i, y_i) mit i = 1,...,n ergeben sich die neuen Rangdaten (rg (x_i), rg (y_i)) mit i = 1,...n.
Die Korrelation wird somit nur auf Grund von Ranginformationen geschätzt, sie ist also auch verwendbar, wenn die Daten schon oder nur als Ränge vorliegen.

Falls innerhalb der x-Werte oder innerhalb der y-Werte identische Werte auftreten (so genannte Bindungen oder "Ties"), werden Durchschnittsränge berechnet, d.h. den identischen Messwerten wird als Rang das arithmetische Mittel der in Frage kommenden Ränge zugewiesen.

Spearmans Korrelationskoeffizient ist nun der auf die Rangpaare angewandte Bravais-Pearson-Korrelationskoeffizient und wird nach folgender Formel berechnet:

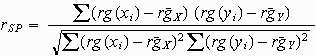
Formel Spearmans Korr.koeffizient

Die Mittelwerte der Ränge sind gegeben durch:

S. K. kann Werte von -1 bis +1 annehmen. Das bedeutet im Einzelnen:

r_SP > 0: gleichsinniger monotoner Zusammenhang (Tendenz: wenn x groß wird, wird auch y groß bzw. wenn x klein wird, wird auch y klein);
r_SP < 0: gegensinniger monotoner Zusammenhang (Tendenz: wenn x groß wird, wird y klein bzw. wenn x klein wird, wird y groß);
r_SP ≈ 0: kein monotoner Zusammenhang

Wenn im Datensatz keine Bindungen auftreten, lässt sich r_SP einfacher berechnen. Dazu müssen erst die Differenzen d_i=rg (x_i) - rg (y_i) bestimmt und dann in die Formel eingesetzt werden: