Rasch-Modell

Das R.-M. ist ein Skalierungsverfahren oder Messmodell, welches eine überprüfbare (mathematische) Theorie über den Zusammenhang zwischen einem zu messenden (latenten) Merkmal und den Antworten von Personen auf Items formuliert. Für binäre (zweiwertige) Items wird angenommen, dass die Antwortwahrscheinlichkeit durch eine logistische Funktion

$y = \frac{e^{x}}{1 + e^{x}}$

beschrieben werden kann. Die Schwierigkeit von Items wird durch den sog. Itempararameter angegeben; das ist der Punkt auf der latenten Variablen, bei dem die Wahrscheinlichkeit einer positiven Antwort 0,5 beträgt. Unterschiedliche Items unterscheiden sich nur durch ihre Schwierigkeit; ansonsten hat ihre Itemcharakteristik die gleiche Form (was u.a. heißt, dass alle Items die gleiche Trennschärfe haben, sofern das Modell für den betreffenden Test/die betreffende Itembatterie überhaupt gilt). Die folgende Graphik zeigt drei Items mit unterschiedlicher Schwierigkeit (bei -1, 0 und 2):

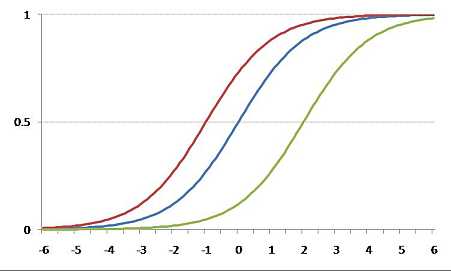
Graphik: Drei Rasch-Itemcharakteristiken

Ein zweiter Parameter, der Personenparameter, gibt die Ausprägung der Untersuchungspersonen auf der gemessenen (latenten) Variablen an. Ist das Rasch-Modell für den Test bzw. die Itembatterie gültig, so besteht ein sehr starker Zusammenhang zwischen dem Summenscore einer Person und dem Personenparameter.

Das Rasch-Modell wurde inzwischen weiterentwickelt; so kann man es auch auf ordinalskalierte Merkmale anwenden und außerdem »mixed Rasch-Modelle« schätzen, bei denen Personen in verschiedene Gruppen klassifiziert und innerhalb dieser Klassen quantitative Personenvariable gemessen werden.

Literatur:

Andrich, David: Rasch Models for Measurement (Sage Series: Quantitative Applications in the Social Sciences, Band 68). Newbury Park, CA: Sage, 1988
Rost, Jürgen: Lehrbuch Testtheorie – Testkonstruktion. 2., vollständig überarbeitete und erweiterte Auflage. Bern u.a.: Hans Huber, 2004