Ordinales Logit-Modell (engl.: Ordered Logit Model)

Das O. L.-M. stellt eine Erweiterung des Verfahrens der binären logistischen Regression auf eine kategoriale abhängige Variable mit mehr als zwei geordneten Ausprägungen dar.

Es gibt einige Varianten ordinaler Logit-Modelle. Die wohl wichtigste und zumeist in den einschlägigen Statistik-Paketen implementierte Variante bezieht sich auf die sog. kumulativen Odds bzw. Logits

bzw.

Es wird also die Wahrscheinlichkeit, in die Kategorien 1 bis i einer abhängigen Variablen mit I Ausprägungen zu fallen, zur Wahrscheinlichkeit in Beziehung gesetzt, in die Kategorien i+1 bis I zu fallen.

Die entsprechende Regressionsgleichung lautet dann:

Es wird also für jede unabhängige Variable ein Regressionskoeffizient geschätzt, allerdings gibt es mehrere Regressionskonstanten b_0i, die sich auch als Schwellenwerte zwischen den Kategorien der abhängigen Variablen interpretieren lassen. (Die genaue Parametrisierung dieser Regressionskonstanten unterscheidet sich teilweise zwischen verschiedenen Statistik-Paketen.) Für die Prüfung der Annahme, dass die Effekte der unabhängigen Variablen auf alle kumulativen Logits gleich sind, wurden Tests entwickelt, die jedoch bei großen Fallzahlen fast immer zur Widerlegung der Null-Hypothese gleicher Effekte führen.

Die Schätzungen des Modells können auch herangezogen werden, um folgende (modellabhängige) Wahrscheinlichkeiten zu berechnen:

und

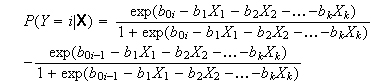
Ordinales Logit, Effekte auf P(y gleich i)

Bei letzterer Formel ist für die erste Kategorie (i=1) der Ausdruck nach dem Minuszeichen gleich 0 und für die letzte Kategorie (i=I) der Ausdruck vor dem Minuszeichen gleich 1.

Die Regressionsparameter werden auf der Grundlage des Maximum Likelihood-Verfahrens geschätzt. Inferenzstatistische Verfahren stehen sowohl für die einzelnen Regressionskoeffizienten als auch für das Gesamtmodell zur Verfügung (siehe Wald-Statistik und Likelihood-Verhältnis-Test); in Analogie zum linearen Regressionsmodell wurden auch Verfahren der Regressionsdiagnostik entwickelt, anhand derer einzelne Fälle mit übergroßem Einfluss auf das Ergebnis der Modellschätzung identifiziert werden können (solche Verfahren sind leider in kaum einem Statistik-Paket implementiert). Schließlich gibt es auch einige Vorschläge zur Berechnung einer Größe, die in Analogie zum R² der linearen Regression eine Abschätzung der »erklärten Varianz« erlaubt; man spricht hier von sog. Pseudo-R². Auch das AIC und das BIC werden in diesem Kontext gelegentlich herangezogen.

Literatur:

Analysis of Ordinal Categorical Data. New York: Wiley, 1984
Agresti, Alan: Categorical Data Analysis. New York: Wiley, 1990, 2. Auflage 2002
Clogg, C. C./Shihadeh, E. S.: Statistical Models for Ordinal Variables. Thousand Oaks, CA:Sage, 1994 (Series: Quantitative Applications in the Social Sciences, Bd. 138)