Kerndichteschätzer (engl.: Kernel Density Estimator)

Ein Kerndichteschätzer ist ein Verfahren, mit dessen Hilfe aus Datenwerten einer Stichprobe die zugrundeliegende Verteilung des betreffenden Merkmals geschätzt werden soll. Es kann nur eingesetzt werden, wenn es sich um ein (zumindest der Theorie nach) stetiges Merkmal handelt (und damit a fortiori um ein metrisches Merkmal, siehe Messniveau). Die Werte des Schätzers werden graphisch dargestellt.

Konkret wird so vorgegangen: Über jedem der erhobenen Datenwerte wird eine stetige Funktion abgetragen, die als Kern bezeichnet wird, und die selbst als Dichte aufgefasst werden kann. Diese sich überlagernden Kerne werden dann aufsummiert; das Ergebnis ist der Kerndichteschätzer.

Die Kerne können im Grunde beliebig gewählt werden, sofern man für die Wahl Gründe angeben kann. Voreinstellung der meisten etablierten Statistikpakete ist der parabelförmige Epanechnikov-Kern (nach W. A. Jepanetschnikow); dieser hat die Eigenschaft, die mittlere quadratische Abweichung des zugehörigen Kerndichteschätzers zu minimieren. In der Praxis zeigt sich, dass die Wahl des Kerns meist keinen großen Einfluss hat. Wichtiger ist die Bandbreite (engl. bandwidth), ein frei zu wählender Glättungsfaktor, der bestimmt, wie sehr der Schätzer auf einzelne Datenpunkte (also u.U. auch Lücken zwischen diesen) reagiert. Es gibt auch hierfür Empfehlungen, die sich in den Voreinstellungen von Software niedergeschlagen, aber in der Praxis kann es ratsam sein, unterschiedliche Bandbreiten auszuprobieren.

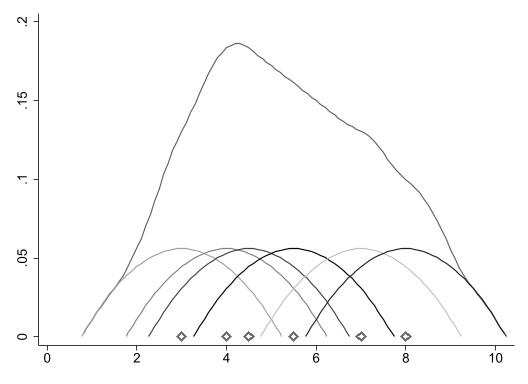
Das folgende Beispiel veranschaulicht das Vorgehen anhand eines (unrealistisch kleinen!) Beispiels. Über den sechs Datenpunkten (durch »Diamanten« gekennzeichnet) ist jeweils ein Epanechnikov-Kern abgetragen. Summiert man an einer gewissen Anzahl von Punkten auf der x-Achse die Kerne und verbindet die Summenwerte wiederum durch eine Kurve, so ergibt sich der (die Kerne überlagernde) Kerndichteschätzer. Im Beispiel ist zu erkennen, dass die Daten auf eine linkssteile Verteilung hindeuten.

© W. Ludwig-Mayerhofer | Last update: 02 Feb 2025