Intraklassenkorrelation (engl.: Intra-Class Correlation)

Die Intraklassenkorrelation (ICC) ist ein Maß der Beobachtungsübereinstimmung und damit ein Indikator der Reliabilität des zugrundeliegenden Beobachtungssystems. Sie setzt intervallskalierte Beobachtungsdaten voraus (s. Messniveau). Im Unterschied zur Produkt-Moment-Korrelation (r_x,y) ist die ICC auch für mehr als zwei Beobachter definiert; sie sollte selbst im Falle zweier Beobachter der Produkt-Moment-Korrelation vorgezogen werden, wenn die Beobachter den Variablen x und y nicht eindeutig zugeordnet werden können (z.B. weil eine Gruppe in wechselnden Dyaden beobachtet hat).

Die ICC basiert auf einem varianzanalytischen Ansatz. Man unterscheidet zwischen

der Varianz zwischen den Beobachtungsfällen, die teilweise auf eine systematische Merkmalsvariation zurückgeführt wird,
der Varianz innerhalb der Beobachtungsfälle, die auf eine mangelhafte Beobachterübereinstimmung hinweist (man spricht daher auch von Fehlervarianz).

Sind die Unterschiede zwischen den Beobachtungsfällen relativ groß bei gleichzeitig geringer Varianz innerhalb der Beobachtungsfälle, so kann von einer reliablen Beobachtung ausgegangen werden.

Die ICC wird gebildet aus dem Quotienten aus

der Differenz der Varianzen »zwischen« und »innerhalb« (man spricht auch von systematischer Varianz, weil die Störvarianz abgezogen wird)
der Summe der Varianz »zwischen« und der (gewichteten) Varianz »innerhalb« (entspricht der Gesamtvarianz).

Im Falle zweier Beobachter (k=2) vereinfacht sich diese Formel zu:

Die Varianzen werden durch mittlere Quadratsummen (MS; Abweichungsquadrate relativiert an Freiheitsgraden) wie folgt geschätzt:

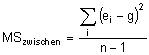
Formel MS zwischen

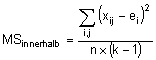
Formel MS innerhalb

Notationshinweise:
n: Anzahl der Beobachtungsfälle (Laufindex: i)
k: Anzahl der Beobachter (Laufindex: j)
x_ij: Beobachtungswert von Beobachter j im Beobachtungsfall i
e_i: Mittelwert eines Beobachtungsfalles i
g: Mittelwert aller Beobachtungswerte x_ij

Die ICC ist 1 (perfekte Reliabilität), wenn MS_innerhalb = 0, d.h. wenn die Beobachter immer gleich beobachtet haben. Die ICC ist 0 (keine Reliabilität), wenn MS_zwischen = MS_innerhalb, d.h. die Varianz zwischen den Beobachtungsfällen diejenige innerhalb der Fälle nicht übersteigt. Im dem Fall, dass MS_zwischen < MS_innerhalb, wird die ICC negativ (was aber in der Praxis nicht häufig vorkommt).

Die bisher diskutierten Formeln verlangen von den Beobachtern absolute Übereinstimmung; man kann hier auch von unjustierter Reliabilität sprechen. Unter bestimmten Voraussetzungen genügt aber auch »relative« Übereinstimmung. Damit ist gemeint, dass die Beobachter unterschiedliche Mittelwerte aufweisen können, und perfekte Reliabilität vorliegt, wenn die den Fällen zugeschriebenen Werte bei allen Ratern in gleicher Weise vom jeweiligen beobachterspezifischen Mittelwert abweichen. Hier kann man von adjustierter Reliabilität sprechen. Die Mittelwertunterschiede zwischen den Ratern werden in diesem Fall nicht bei der Fehlervarianz berücksichtigt.

Schließlich kann man noch zwischen der Reliabilität eines einzelnen »mittleren« Beobachters und der Reliabilität der gesamten Beobachtergruppe differenzieren. Letztere Form der Reliabilität sollte man nur dann heranziehen, wenn auch später in der Anwendungspraxis (z. B. bei der Beurteilung von Patienten) die gesamte Beobachtergruppe zum Einsatz kommt.

Literatur:

Asendorpf, J./Wallbott, H.G.: Maße der Beobachterübereinstimmung: Ein systematischer Vergleich. In: Zeitschrift für Sozialpsychologie, 10, 1979, 243-252
Greve, W./Wentura, D.: Wissenschaftliche Beobachtung. Eine Einführung. Weinheim: Psychologie Verlags Union, 1997
McGraw, K. O./Wong, S. P.: Forming Inferences About Some Intraclass Correlation Coefficients, in: Psychological Methods 1, 1996, S. 30-46
Shrout, P. E./Fleiss, J. L.: Intraclass Correlations: Uses in Assessing Rater Reliability, in: Psychological Bulletin 86, 1979, S. 420-42
Wirtz, Markus/Caspar, Franz: Beurteilerübereinstimmung und Beurteilerreliabilität. Methoden zur Bestimmung und Verbesserung der Zuverlässigkeit von Einschätzungen mittels Kategoriensystemen und Ratingskalen. Göttingen, Bern, Toronto, Seattle: Hogrefe, 2002.