Zufallsvariable (manchmal auch: Zufallsgröße) (engl: Random Variable)

Man spricht von einer Z., wenn die numerischen Werte (Ausprägungen), die ein Merkmal annimmt, Ergebnisse eines Zufallsvorgangs sind. Diese Werte können konkrete Ereignisse sein (etwa die Zahlen 1, 2 usw. als Ergebnisse des Würfelns); zumeist interessiert man sich jedoch für aus diesen Ereignissen abgeleitete Zahlen, etwa »die Häufigkeit einer Zahl größer als 3 bei mehmaligem Würfeln«. Man kann dann sagen, dass die Z. eine Funktion (über den Ereignisraum) ist, die den Ergebnissen des Zufallsvorganges reelle Zahlen zuordnet.

Für die Inferenzstatistik ist die Vorstellung zentral, dass Stichprobenkennwerte (z.B. Mittelwerte, Anteilswerte, Streuungen in einer Stichprobe) als Z.n charakterisiert werden können (immer vorausgesetzt, dass die Kennwerte einer Zufallsstichprobe entstammen).

Z.en können diskret oder stetig sein. Erstere werden durch eine Wahrscheinlichkeitsfunktion, letztere durch eine Dichtefunktion gekennzeichnet; aus beiden Funktionen ergibt sich jeweils auch die eine Variable kennzeichnende Verteilungsfunktion.

Der Erwartungswert einer Z. gibt ihr Zentrum oder ihre Lage an. Er ist analog dem arithmetischen Mittel einer empirischen Variablen zu verstehen, doch bezieht er sich gerade nicht auf gegebene Daten, sondern auf ein theoretisch erwartetes Verhalten eines Zufallsvorgangs. Der Erwartungswert wird meist als E(X) oder auch mit dem griechischen Buchstaben μ (sprich: mü) bezeichnet.

Bei einer diskreten (aber metrischen) Zufallsvariablen (auch binäre Variablen darf man analog behandeln) entspricht der Erwartungswert der Summe der mit den Wahrscheinlichkeiten gewichteten Ausprägungen:
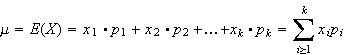
Erwartungswert einer diskreten Zufallsvariablen
Wirft man beispielsweise eine Münze vier Mal und ordnet dem Ereignis "Kopf" den Wert 1 zu, so beträgt der Erwartungswert:

E(X) = 0 x 0,0625 + 1 x 0,25 + 2 x 0,375 + 3 x 0,25 + 4 x 0,0625 = 2.

(Zur Berechnung der angegebenen Wahrscheinlichkeiten siehe Binomialverteilung). Man erwartet also zwei Mal "Kopf". Das gleiche Ergebnis ergibt sich auch intuitiv anhand der Summe der Wahrscheinlichkeiten für Kopf je Wurf (4 x 0,5).

In analoger Weise kann man bei einer stetigen Z. den Erwartungswert durch Integrieren bilden:

Die Varianz einer Z. kann man ebenfalls in Analogie zu empirischen Merkmalen als Streuung (um den Erwartungswert) beschreiben. Sie beträgt bei einer diskreten Z.
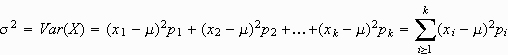
Varianz einer diskreten Zufallsvariablen
und bei einer stetigen Z.