Verteilungsfunktion

Die V. gibt den Anteil der Werte einer Variablen an, die kleiner oder gleich einem gegebenen Wert x sind.

Handelt es sich bei dieser Variablen um eine Zufallsvariable, so gibt die V. die Wahrscheinlichkeiten an, dass die Werte der Variablen kleiner gleich x sind; formal:

Konkret heißt das im Fall einer diskreten Zufallsvariablen:

also die Summe aller Einzelwahrscheinlichkeiten mit x_i kleiner gleich x, und im Fall einer stetigen Zufallsvariablen:

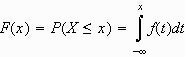Stetige Verteilungsfunktion ,

also das unbestimmte Integral der Wahrscheinlichkeitsdichte von minus unendlich bis zur Stelle x.

Handelt es sich dagegen um empirische Daten (Messwerte), so spricht man von der empirischen Verteilungsfunktion

also der Summe der relativen Häufigkeiten der Ausprägungen a_i bis zum Wert a_j=x (wobei angenommen wird, dass es sich um eine ordinalskalierte oder metrische Variable handelt). Anders gesagt handelt es sich bei der empirischen V. um die kumulierte Häufigkeitsverteilung einer Reihe von Messwerten.

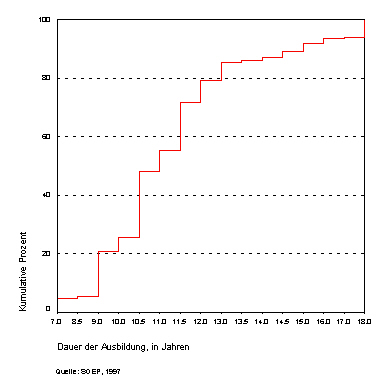
Die nachfolgende Grafik (nach Daten aus dem SOEP 1997) zeigt als Beispiel einer empirischen V. die Verteilung von "Bildungsinvestitionen", gemessen als (typische) Dauer bis zum Erreichen des höchsten schulischen und beruflichen Abschlusses der Untersuchungspersonen. Man kann aus der Grafik z. B. ablesen, dass ca. 6 Prozent der Untersuchungspersonen nicht mehr als 7 Jahre Bildung aufweisen können, etwas über 20. Prozent haben nicht mehr als 9 Jahre, knapp 50 Prozent nicht mehr als 10,5 Jahre, usw.

Empirische Verteilungsfunktion