Maximum Likelihood-Schätzung (engl.: Maximum Likelihood Estimation)

Die Maximum Likelihood-Schätzung, oft einfach als ML-Schätzung (englisch: MLE) bezeichnet, ist ein statistisches Schätzverfahren, das bei größeren Stichproben asymptotisch unverzerrte, effiziente, konsistente, normalverteilte Schätzer liefert. Es handelt sich um eines der grundlegenden Schätzverfahren der modernen Statistik. Ihre Entwicklung geht auf R. A. Fisher zurück.

Die Logik des Verfahrens lässt sich wie folgt beschreiben: Gegeben sind Daten einer Stichprobe und Annahmen über die Verteilung der relevanten Variablen. Geprüft wird nun, bei welchem (oder welchen) Parameter(n) in der Grundgesamtheit die gegebenen Daten mit der größten Wahrscheinlichkeit auftreten würden; der betreffende Wert gilt dann als bester Schätzer für den oder die Parameter. Es muss also das Maximum einer Funktion gefunden werden, die sich auf diese Wahrscheinlichkeiten bezieht, daher der Name Maximum Likelihood. Die betreffende Funktion heißt Likelihood-Funktion.

Diese Idee sei an einem einfachen Beispiel erläutert, nämlich einer binomialverteilten Variablen Y mit den Ausprägungen 0 und 1. Die Wahrscheinlichkeit P dieser beiden Ausprägungen ist für ein einzelnes Stichprobenelement bei gegebenem Parameter π

$P (y | π) = π^{y} \cdot {(1 - π)}^{1 - y}$

ein Ausdruck, der sich für Y = 1 auf π und für Y = 0 auf 1-π reduziert.

Bei der Maxikum-Likelihood-Schätzung betrachten wir nicht die Datenwerte als zufällige Realisierung eines (fixen) Parameters, sondern suchen umgekehrt nach dem Parameter, der bei gegebenen Daten die größte «Wahrscheinlichkeit« besitzt. Im Beispiel wird also der Parameter π variiert, und gesucht wird derjenige Wert, der (bei einer Stichprobe vom Umfang n, in der mit Häufigkeit k der Wert Y = 1 beobachtet wurde) den folgenden Ausdruck maximiert, der die Likelihood als Produkt der einzelnen Wahrscheinlichkeiten beschreibt:

$L (π; y_{1}, . . ., y_{n}) = \prod π^{y_{i}} \cdot {(1 - π)}^{1 - y_{i}} = π^{k} \cdot {(1 - π)}^{n - k}$

Die folgenden Graphik zeigt die Werte der Likelihood unterschiedlicher Werte von π für den Fall n = 10 und k = 2. Das Maximum der Likelihood liegt bei π = 0,2.

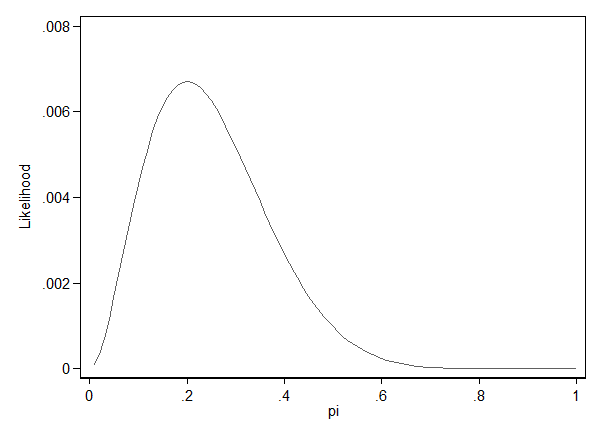
Plot einer Likelihood für n = 10 und k = 2

Da die Likelihood ein Produkt einzelner Wahrscheinlichkeiten ist, führt sie bei großen Stichproben – und nur in großen Stichproben sind die ML-Schätzer (asymptotisch) gültig – zu sehr winzigen und daher auch mit modernen Computern schwer zu traktierenden Größen. In der Praxis wird daher der Logarithmus der Likelihood, die sog. Log-Likelihood maximiert, die sich aufgrund der Logarithmierung nicht als Produkt, sondern als Summe darstellen lässt. Die Log-Likelihood, genauer gesagt: die Größe − 2*Log-Likelihood (oft als − 2LL abgekürzt) ist auch wichtig für die inferenzstatistische Beurteilung des Modells bzw. den Modellvergleich (siehe Likelihood-Verhältnis-Test).

Die Schätzung wird in der Regel mittels iterativer Methoden durchgeführt, für die auch die erste und zweite Ableitung der Likelihood-Funktion benötigt werden. Die zweite Ableitung liefert insbesondere auch die Standardfehler für die geschätzten Koeffizienten.

In der Praxis können u. a. folgende Probleme auftreten:
1. Die Likelihood-Funktion kann bei manchen Verteilungen mehrere (lokale) Maxima haben. Hier ist nicht sichergestellt, daß tatsächlich das absolute Maximum gefunden wird.
2. Manchmal hat (bei gegebenen Daten) die Likelihood-Funktion tatsächlich kein Maximum und die (iterative) Schätzung konvergiert nicht. Manche Programme teilen den Benutzern mit, wenn dieser Fall vorzuliegen scheint; andere (so SPSS) behelfen sich teilweise mit (nicht näher erläuterten) Tricks (man kann dann Parameter, die eigentlich gar nicht geschätzt werden können, an übergroßen Standardfehlern erkennen).

Literatur:

Gautschi, Thomas: Maximum-Likelihood Schätztheorie, in: Wolf, Christof/Best, Henning (Hrsg.): Handbuch der sozialwissenschaftlichen Datenanalyse. Wiesbaden: VS Verlag für Sozialwissenschaften, 2010, S. 205-235.

Siehe auch: Likelihood-Funktion; Likelihood-Verhältnis-Test.