Quantil-Plot (engl. Quantile Plot)

Verfahren der graphischen Darstellung von Häufigkeitsverteilungen. Q-P.s gehören zum Standardwerkzeug der explorativen Datenanalyse. Mit ihrer Hilfe kann die Streuung von Daten um ihr Zentrum charakterisiert werden; sie erlauben Aussagen über die Symmetrie einer Verteilung und über mögliche Ausreißer. Ebenso lassen sich mit Q.-P.s zwei unterschiedliche Verteilungen miteinander vergleichen. Dazu werden (je nach Art des Quantil-Plots) bestimmte Quantile empirischer und/oder theoretischer Verteilungen in einem Koordinatensystem abgetragen.

Es lassen sich verschiedene Arten von Quantil-Plots unterscheiden:

In einem einfachen Quantil-Plot sind auf der x-Achse verschiedene Quantile, nach denen sich ein der Größe nach geordnetes Datenbündel teilen lässt, z. B. das 0,25-, 0,5- und 0,75-Quartil, abgetragen, auf der y-Achse die Datenwerte. Weisen die Daten nun an jeder Stelle dieselbe Dichte auf bzw. sind die Daten gleichverteilt, entspricht die Kurve des Quantil-Plots der Winkelhalbierenden. Diese Situation wird sich in der Realität jedoch selten finden.

Entspricht die Verteilung der Daten annähernd einer Normalverteilung ergibt sich ein umgekehrt S-förmiger Kurvenverlauf. Handelt es sich um eine rechtsschiefe (linksschiefe) Verteilung, ergibt sich ein zunächst langer flacher (kurzer steiler), zum Schluss stark ansteigender (langsam ansteigender) Verlauf. Es gilt: Bereiche mit starker Steigung bedeuten geringe Datendichte und umgekehrt.

Der folgende Plot zeigt die Verteilung der Angaben zur Wohnfläche in qm aus dem Sozio-ökonomischen Panel. Man erkennt, dass ein kleiner Teil der Wohnungsflächen (wohl unter 5 Prozent) in einem Bereich von etwa 10 bis 30 qm liegt; die große Masse (etwa zwischen dem 5. und dem 80. Perzentil) liegt zwischen 40 und 100 qm. Wohnungsgrößen von 150 bis 400 qm machen nur einen kleinen Teil (wenige Prozente) am oberen Ende der Verteilung aus.

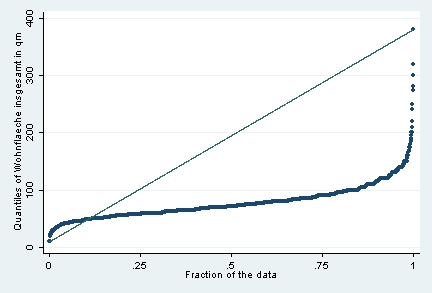
einfacher Quantilplot
Quantil-Plot, Variable »Wohnfläche insgesamt in qm«, SOEP 2002

Eine Variante dazu stellen Quantil-Quantil-Plots (QQ-Plots) dar, die zum Vergleich zweier Verteilungen herangezogen werden können. Dazu werden ausgewählte Quantile der beiden Verteilungen gegeneinander abgetragen. Empirische QQ-Plots vergleichen zwei empirische Verteilungen; theoretische QQ-Plots erhält man dagegen, wenn eine der empirischen Verteilungen durch eine theoretische ersetzt wird und die Quantile der Daten gegen die entsprechenden Quantile der theoretischen Verteilung geplottet werden.

Liegen die Punkte an oder in der Nähe der Winkelhalbierenden, sind die beiden Verteilungen in etwa gleich. Verläuft der Graph parallel zur Winkelhalbierenden, unterscheiden sich die beiden Verteilungen nur durch den Lageparameter; weist die Verteilung, die entlang der x-Achse abgetragen ist, eine größere Varianz auf, verläuft die Kurve flacher als die Winkelhalbierende. So können bspw. die Einkommensverteilungen von Männern und Frauen verglichen werden.

Im folgenden empirischen QQ-Plot ist deutlich zu erkennen, dass das Einkommen der Männer über demjenigen der Frauen liegt: Die Punkte liegen konstant über der Winkelhalbierenden; dasjenige (in dieser Variante nicht bestimmbare) Quantil, dessen Wert bei den Frauen bei etwa 5000 Euro liegt, hat bei den Männern schon einen Wert von etwa 10000 Euro.

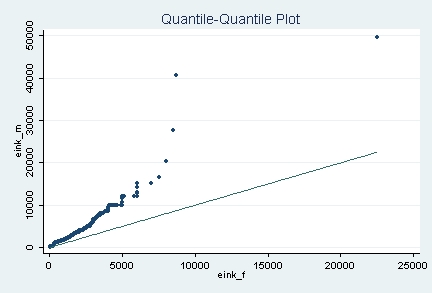
QQ-Plot
QQ-Plot, Variablen »Einkommen Frauen« und »Einkommen Männer«, SOEP 2002

Ein wichtiger Anwendungsbereich theoretischer QQ-Plots ist der Vergleich einer empirischen Verteilung mit einer (theoretischen) Normalverteilung in sog. Normal-Quantil-Plots. Hier werden die Quantile einer empirischen Häufigkeitsverteilung mit entsprechenden Quantilen der Normalverteilung verglichen. Dieses Verfahren ist deshalb von Bedeutung, da viele statistische Verfahren voraussetzen, dass eine (approximative) Normalverteilung vorliegt; diese Bedingung kann also mit dem Normal-Quantil-Plot geprüft werden.

Bei Übereinstimmung der beiden Verteilungstypen liegen die Punkte in etwa auf der Winkelhalbierenden. Bei Nichtübereinstimmung lässt sich die Art der Abweichung aus dem Graphen bestimmen. Bestehen lediglich Abweichungen bezüglich der Lage (Verweis)- und Streuungsparameter (Verweis), bleibt die Form der Geraden erhalten. Eine S-förmige (umgekehrt S-förmige) Kurve deutet auf eine im Vergleich zur Normalverteilung stärker gewölbte (spitzere) Verteilung hin. Eine konkave (konvexe) Kurve ergibt sich bei rechtsschiefer (linksschiefer) Verteilung der Daten.

Im Diagramm wird jeder beobachtete Wert (auf der y-Achse) mit seinem unter Nomalverteilung erwarteten Wert (x-Achse) gepaart (die Einheiten orientieren sich hier an den Einheiten der empirischen Verteilung; es gibt auch Plots, in denen die erwarteten Werte in standardisierter Form abgetragen werden; außerdem finden sich manchmal, z.B. bei SPSS, die beobachteten Werte auf der x-Achse).

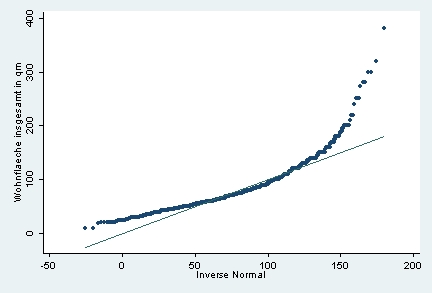
Normal-Quantil-Plot, Variable »Wohnfläche insgesamt in qm«, SOEP 2002

Eine weitere Variante, um Abweichungen einer Verteilung von der Normalverteilung aufzuspüren, stellen sog. Normalwahrscheinlichkeitsplots (normal probability plots) dar. Im Gegensatz zu den Normal-Quantil-Plots, die die Enden einer Verteilung betonen, wird hier der Mitte der Verteilung größere Beachtung geschenkt.

In diesem Diagramm werden die beobachteten kumulierten Wahrscheinlichkeiten auf der x-Achse gegen die erwarteten kumulierten Wahrscheinlichkeiten auf der y-Achse abgetragen.

Die Kurve zeigt, dass sich die empirischen Daten im ersten Viertel der Verteilung stärker konzentrieren als es bei einer Normalverteilung zu erwarten wäre, während die Mitte deutlich schwächer besetzt ist als wenn die Daten normalverteilt wären.

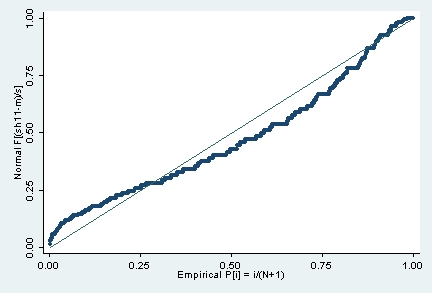
Normal-Probability-Plot, Variable »Wohnfläche insgesamt in qm«, SOEP 2002

Literatur:

Heiler, Siegfried/Michels, Paul: Deskriptive und explorative Datenanalyse. München, Wien: Oldenbourg 1994